 Решение уравнений и неравенств с модулем часто вызывает затруднения. Однако, если хорошо понимать, что такое модуль числа, и как правильно раскрывать выражения, содержащие знак модуля, то наличие в уравнении выражения, стоящего под знаком модуля, перестает быть препятствием для его решения.
Решение уравнений и неравенств с модулем часто вызывает затруднения. Однако, если хорошо понимать, что такое модуль числа, и как правильно раскрывать выражения, содержащие знак модуля, то наличие в уравнении выражения, стоящего под знаком модуля, перестает быть препятствием для его решения.
Немного теории. Каждое число имеет две характеристики: абсолютное значение числа, и его знак.
Например, число +5, или просто 5 имеет знак "+" и абсолютное значение 5.
Число -5 имеет знак "-" и абсолютное значение 5.
Абсолютные значения чисел 5 и -5 равны 5.
Абсолютное значение числа х называется модулем числа и обозначается |x|.
Как мы видим, модуль числа равен самому числу, если это число больше или равно нуля, и этому числу с противоположным знаком, если это число отрицательно.
Это же касается любых выражений, которые стоят под знаком модуля.
Правило раскрытия модуля выглядит так:
|f(x)|= f(x), если f(x) ≥ 0, и
|f(x)|= - f(x), если f(x) < 0
Например |x-3|=x-3, если x-3≥0 и |x-3|=-(x-3)=3-x, если x-3<0.
Чтобы решить уравнение , содержащее выражение, стоящее под знаком модуля, нужно сначала раскрыть модуль по правилу раскрытия модуля.
Тогда наше уравнение или неравенство преобразуется в два различных уравнения, существующих на двух различных числовых промежутках.
Одно уравнение существует на числовом промежутке, на котором выражение, стоящее под знаком модуля неотрицательно.
А второе уравнение существует на промежутке, на котором выражение, стоящее под знаком модуля отрицательно.
Рассмотрим простой пример.
Решим уравнение:
|x-3|=-x2+4x-3
1. Раскроем модуль.
|x-3|=x-3, если x-3≥0, т.е. если х≥3
|x-3|=-(x-3)=3-x, если x-3<0, т.е. если х<3
2. Мы получили два числовых промежутка: х≥3 и х<3.
Рассмотрим, в какие уравнения преобразуется исходное уравнение на каждом промежутке:
А) При х≥3 |x-3|=x-3, и наше уранение имеет вид:
x-3=-x2+4x-3
Внимание! Это уравнение существует только на промежутке х≥3!
Раскроем скобки, приведем подобные члены:
x2 -3х=0
и решим это уравнение.
Это уравнение имеет корни:
х1=0, х2=3
Внимание! поскольку уравнение x-3=-x2+4x-3 существует только на промежутке х≥3, нас интересуют только те корни, которые принадлежат этому промежутку. Этому условию удовлетворяет только х2=3.
Б) При x<0 |x-3|=-(x-3) = 3-x, и наше уравнение приобретает вид:
3-x=-x2+4x-3
Внимание! Это уравнение существует только на промежутке х<3!
Раскроем скобки, приведем подобные члены. Получим уравнение:
x2-5х+6=0
х1=2, х2=3
Внимание! поскольку уравнение 3-х=-x2+4x-3 существует только на промежутке x<3, нас интересуют только те корни, которые принадлежат этому промежутку. Этому условию удовлетворяет только х1=2.
Итак: из первого промежутка мы берем только корень х=3, из второго - корень х=2.
Ответ: х=3, х=2
























Здравствуйте,Инна.Как умножить модуль на квадратное уравнение?
Спасибо.
Нужно раскрыть модуль: рассмотреть случаи, когда подмодульное выражение больше нуля и когда меньше нуля.
Если модуль в модуле. ||x| — 1| * |x| / x^2 — 1 ==> x -(x + 1) * (-x) / (x^2 — 1) ==> x(x + 1) / (x — 1)(x + 1) = ==> x/ x — 1.
-1 < x |-x — 1| * (-x) / (x^2 — 1) ==> -(x + 1) * (-x) / (x^2 — 1) ==> x(x + 1) / (x — 1)(x + 1) = ==> x/ x — 1.
0 <= x -(x — 1) * x / (x^2 — 1) ==> -x(x — 1) / (x^2 — 1) ==> x(x + 1) / (x — 1)(x + 1) = ==> x/ x — 1.
Не до конца понимаю, как правильно раскрыть модуль в модуле, и, соответственно, какой знак внутри модуля в который вложен другой модуль…
В этом примере проще ввести замену: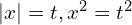 , тогда получится выражение с одним модулем. В общем случае сначала раскрываем внутренний модуль, потом внешний. При раскрытии модуля необходимо указывать промежуток, на котором мы находимся. Например:
, тогда получится выражение с одним модулем. В общем случае сначала раскрываем внутренний модуль, потом внешний. При раскрытии модуля необходимо указывать промежуток, на котором мы находимся. Например: 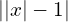 . Cначала рассматриваем случай
. Cначала рассматриваем случай 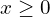 , Получаем систему:
, Получаем систему: 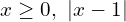 . И теперь система разбивается на совокупность двух систем:
. И теперь система разбивается на совокупность двух систем: 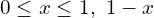 и
и 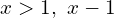 . Так же рассматриваем второй случай, когда
. Так же рассматриваем второй случай, когда 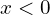 .
.
ОДЗ +- 1;
Внутренний модуль |x| может быть x >= 0, x = 0, |x — 1| = 0, 0 <= x < 1, |x — 1|* x = -x(x — 1)/(x — 1)(x + 1).
Второй случай x < 0 |-(x) — 1| * (-x) = тут мне не ясно, знак -x выносится за скобки или происходит арифметическое действие внутри модуля-скобок т.е. -x — 1 < 0 = -(x + 1)….
Я так решал, но ответ не верен, и, понять, как получается правильный ответ, я не могу.
Здравствуйте, Инна! обязательно ли при раскрытии модуля чередовать знак равно? Например, в первом случае х больше или равно трех, а в другом — строго меньше трех.
Нет, не обязательно. Если конец промежутка входит в область допустимых значений, то его можно включать в оба промежутка.
спасибо большое