В этой статье мы познакомимся с понятием производной функции, с физическим смыслом производной и решим несколько задач из Задания В9 из Открытого банка задач для подготовки к ЕГЭ по математике на использование физического смысла производной.
Чтобы понять, что такое производная, проведем аналогию с мгновенной скоростью. Рассмотрим материальную точку, которая движется по прямой с переменной скоростью. Поскольку скорость точки все время меняется, мы можем говорить о ее скорости только в данный момент времени 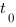 . Чтобы найти скорость точки в момент времени
. Чтобы найти скорость точки в момент времени 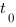 , рассмотрим маленький промежуток времени
, рассмотрим маленький промежуток времени  . За этот промежуток времени точка пройдет расстояние
. За этот промежуток времени точка пройдет расстояние  . Тогда скорость точки будет примерно равна
. Тогда скорость точки будет примерно равна 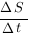 . Чем меньше промежуток времени
. Чем меньше промежуток времени  мы будем брать, тем точнее значение скорости мы получим. В пределе, при
мы будем брать, тем точнее значение скорости мы получим. В пределе, при  , мы получим точное значение мгновенной скорости в момент времени
, мы получим точное значение мгновенной скорости в момент времени 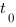 :
:

Аналогичным образом введем понятие производной.
Рассмотрим произвольную функцию  и зафиксируем точку
и зафиксируем точку 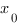 . Значение функции в этой точке равно
. Значение функции в этой точке равно 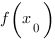 . Возьмем приращение аргумента
. Возьмем приращение аргумента  . Значение функции в этой точке равно
. Значение функции в этой точке равно 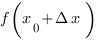 . Получим приращение функции
. Получим приращение функции 
Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:
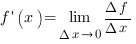
Физический смысл производной.
Итак, мы видим, что по аналогии с мгновенной скоростью, производная функции в точке 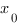 . показывает скорость изменения функции в этой точке.
. показывает скорость изменения функции в этой точке.
Если зависимость расстояния от времени представляет собой функцию  , то, чтобы найти скорость тела в момент времени
, то, чтобы найти скорость тела в момент времени 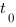 , нужно найти значение производной функции
, нужно найти значение производной функции  в точке
в точке 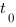 :
:


Пример 1. Решим задание В9 (№ 119975) из Открытого банка заданий для подготовки к ЕГЭ по математике.
Материальная точка движется прямолинейно по закону 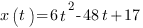 , где
, где 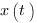 — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах, 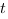 — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени
— время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени  .
.
Решение.
1. Найдем производную функции 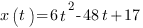 :
:
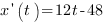
2. Найдем значение производной в точке  :
:


Ответ: 60 м/с.
Пример 2. Решим задание В9 (№ 119978)
Материальная точка движется прямолинейно по закону  , где
, где 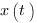 — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах, 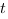 — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 3 м/с?
— время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 3 м/с?
Решение.
Если нам известна скорость точки в некий момент времени , следовательно нам известно значение производной в точке 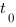 .
.
Найдем производную функции 
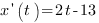
По условию, скорость точки равна 3 м/с, значит, значение производной в момент времени 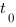 равно 3.
равно 3.
Получаем уравнение:
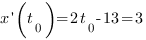
Отсюда  с.
с.
Ответ: 8
Пример 3. Аналогичное задание. Задание В9 (№119979)
Материальная точка движется прямолинейно по закону  , где
, где 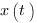 — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах, 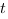 — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 2 м/с?
— время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 2 м/с?
Решение.
Найдем производную функции  :
:

По условию, скорость точки равна 2 м/с, значит, значение производной в момент времени 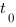 равно 2.
равно 2.
Получаем уравнение:
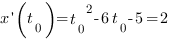
Решим его:


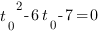
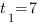 ,
,  - не подходит по смыслу задачи: время не может быть отрицательным.
- не подходит по смыслу задачи: время не может быть отрицательным.
Ответ: 7
























отличная помощь школьникам, коротко и понятно!
А мне кажется это отличная помощь не школьникам, а роботам. Которых учат знать много непонятных слов и запоминать формулы. Если Вы со мной несогласны, то объясните мне смысл производной без этого абстрактного дерьма (простите за грубость): Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю. (прямо представляю какой огонь интереса зажигается в глазах 9ти классника после этой фразы)
Объясните на простых словах, человеку далекому от математики, для чего мне все это надо (желательно с примерами не про скорость «материальной точки» (кстати что это?), а из реальной жизни). И подумайте, часто ли учителя объясняют это своим ученикам.
Хороший вопрос.) А надо вот зачем. Если какой-то процесс описывается некоторой функций, которая выражает зависимость одного параметра от другого, то производная этой функции — скорость этого процесса.
Спасибо, Роман, за идею. Надо писать статьи под рубрикой «зачем это надо»
Есть учащиеся, которые учатся осознанно, интересуются, задают вопросы, развиваются. Есть ученики: принимают только то, что дает учитель, не больше. И есть, как ты говоришь, школьники, которые просто ходят в школу, а не учатся. Вот им ничего не нужно: сидели бы на печи, если бы мамка из дома не выгоняла каждое утро и все. Ты, Рома, кто???
Любовь вы это зря. Правда в том, что в жизни это редко кому пригодится. Я не против знаний. Мой сын Руслан учится на отделении радиоэлектроника. Ему понятно всё и просто. Но большинству ребят не нужны такие глубокие познания. Я до сих пор учусь, правда мне роднее электротехника.Работаю электромехаником на тяговой подстанции.
Думаю для студентов нужный сайт
Спасибо за информацию. Очень люблю точные науки. По жизни — технарь.
Вот интересная статья для понимания производной: ««
Сайт супер!Всё ясно и понятно)
как вы нашли т1 и т2 расскажите подробней?
Нужно решить квадратное уравнение.
Здравствуйте! Подскажите, пожалуйста, а какие действия нужно выполнить, чтобы по заданному уравнению (например, уравнение прямолинейного движения материальной точки x(t)) узнать в какой момент времени t скорость тела V была максимальная?
Берем производную от функции зависимости расстояния от времени, получаем функцию зависимости скорости от времени. И исследуем ее на максимум — минимум.
Спасибо большое!