 Расстояние от точки до плоскости. Метод координат. Задание 14
Расстояние от точки до плоскости. Метод координат. Задание 14
В этой статье мы поговорим о том, как найти расстояние от точки до плоскости с помощью метода координат. О том как находить расстояние от точки до плоскости геометрическим способом, вы можете прочитать здесь.
Решим задачу: в единичном кубе 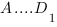 найдите расстояние от точки
найдите расстояние от точки 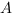 до плоскости
до плоскости 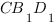 .
.
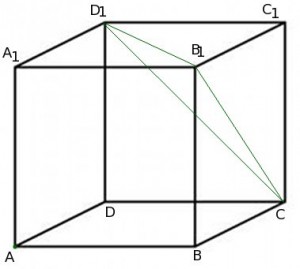
На этот раз давайте решим ее с помощью метода координат.
Сначала немного теории.
Рассстояние 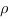 от точки
от точки 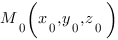 до плоскости
до плоскости  вычисляется по такой формуле:
вычисляется по такой формуле:
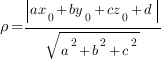
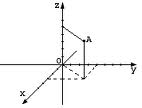
Чтобы воспользоваться этой формулой, поместим наш куб в систему координат:
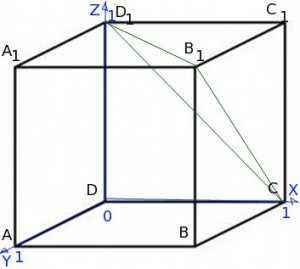 В нашей задаче роль точки
В нашей задаче роль точки 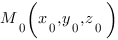 играет точка
играет точка 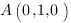 . То есть
. То есть 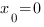 ,
, 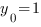 ,
, 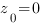
Теперь наша задача найти коэффициенты  ,
,  ,
, 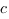 и
и 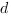 в уравнении
в уравнении  плоскости
плоскости 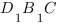 .
.
Плоскость 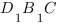 определяется тремя точками
определяется тремя точками 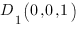 ,
, 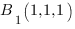 и
и 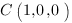 . Если мы координаты точек подставим в уравнение плоскости
. Если мы координаты точек подставим в уравнение плоскости  , то получим верное равенство.
, то получим верное равенство.
Коэффициент 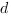 в уравнении плоскости мы можем принять равным 1.
в уравнении плоскости мы можем принять равным 1.
Чтобы найти коэффициенты  ,
,  и
и 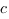 , подставим координаты точек
, подставим координаты точек 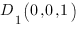 ,
, 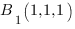 и
и 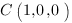 в уравнение плоскости
в уравнение плоскости  . Получим систему уравнений:
. Получим систему уравнений:
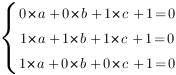
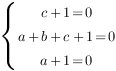
Отсюда: 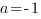 ,
, 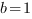 ,
, 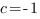
Подставим координаты точки 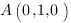 и значения коэффициентов в формулу для расстояния:
и значения коэффициентов в формулу для расстояния:
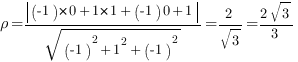
Ответ: 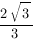
И.В. Фельдман, репетитор по математике.

























Почему d=1 ???
всё, разобрался почему))
Может ли точка, от которой мы ищем расстояние до плоскости,в нашем случае А, иметь координаты (0,0,0)?
Да, конечно
Спасибо
А как найти коэффициент d?
Посмотрите здесь: //ege-ok.ru/2012/03/18/uravnenie-ploskosti/
А разве x не заведует перемещением вперед и назад?у вас на картинке он заведует перемещением точки вправо и влево.
Вы правы, все прямоугольные системы координат в трехмерном пространстве делятся на два класса — правые (также используются термины положительные, стандартные) и левые. Чаще используют правые координатные системы (о которой говорите вы). С точки зрения решения задач это не принципиально.