
Расстояние между скрещивающимися прямыми. Задание 14.
В этой статье мы будем учиться находить расстояние между двумя скрещивающимися прямыми. Мы рассмотрим два геометрических способа. Аналитический способ нахождения расстояния между прямыми ( с помощью метода координат) мы рассмотрим в другой статье.
Как обычно, сначала немного теории.
Расстоянием между скрещивающимися прямыми называется расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой.
То есть, для того, чтобы найти расстояние между двумя скрещивающимися прямыми, нужно
1. Через одну из прямых провести плоскость, параллельную второй прямой.
2. Из любой точки первой прямой опустить перпендикуляр на плоскость и найти его длину. То есть задача сводится к нахождению расстояния от точки до плоскости. Это можно сделать геометрическим методом или с помощью метода координат.
Рассмотрим решение задачи.
В правильной треугольной призме  , все ребра которой равны 1, найдите расстояние между прямыми
, все ребра которой равны 1, найдите расстояние между прямыми  и
и  :
:
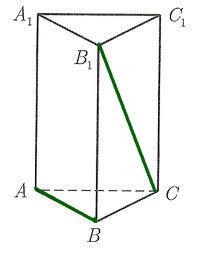 Решение.
Решение.
1 способ.
Прямая  параллельна прямой
параллельна прямой  . Проведем через прямые
. Проведем через прямые  и
и  плоскость
плоскость  , параллельную прямой
, параллельную прямой  :
:
Возьмем точку М, являющуюся серединой отрезка  . Проведем через эту точку плоскость
. Проведем через эту точку плоскость  .
.
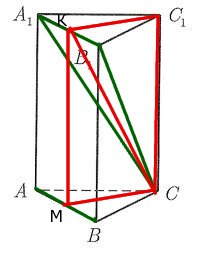
Докажем, что плоскость  перпендикулярна прямой
перпендикулярна прямой  , и, следовательно, плоскости
, и, следовательно, плоскости 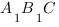 :
:
Отрезок  является медианой, и, следовательно, высотой равностороннего треугольника
является медианой, и, следовательно, высотой равностороннего треугольника  . Прямая
. Прямая  параллельна прямой
параллельна прямой  и, следовательно, перпендикулярна
и, следовательно, перпендикулярна  . То есть прямая
. То есть прямая  перпендикулярна двум пересекающимся прямым плоскости
перпендикулярна двум пересекающимся прямым плоскости  , и, следовательно перпендикулярна плоскости.
, и, следовательно перпендикулярна плоскости.
Теперь рассмотрим в плоскости  прямоугольный треугольник
прямоугольный треугольник  и проведем в нем высоту
и проведем в нем высоту  :
:
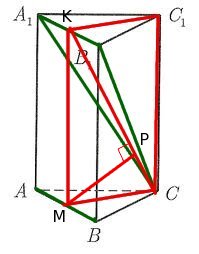 Длина высоты
Длина высоты  треугольника и есть расстояние между прямыми
треугольника и есть расстояние между прямыми  и
и 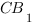 , которой нам нужно найти.
, которой нам нужно найти.
Чтобы найти высоту  , выразим два раза площадь треугольника
, выразим два раза площадь треугольника  .
.






Ответ: 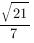
2 способ.
Рассмотрим пирамиду  внутри призмы
внутри призмы  .
.  - высота этой пирамиды. Ее длина - расстояние между прямыми
- высота этой пирамиды. Ее длина - расстояние между прямыми  и
и  .
.

Выразим объем пирамиды  через объем призмы
через объем призмы .
.
Чтобы найти объем пирамиды  , нужно из объема призмы
, нужно из объема призмы 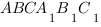 вычесть объемы пирамиды
вычесть объемы пирамиды  ,
,  и
и  .
.
Пусть  - площадь основания призмы
- площадь основания призмы 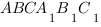 , и
, и 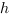 - ее высота. Тогда:
- ее высота. Тогда:



Следовательно, объем пирамиды  равен:
равен:
 =
=



Объем пирамиды 

Отсюда:


Ответ: 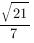
И.В. Фельдман, репетитор по математике.
























Уважаемая Инна Владимировна! Впервые забрела на Ваш сайт. Буду рекомендовать его коллегам и выпускникам. Во втором способе можно рассмотреть объём призмы как сумму объёмов пирамид А1АВС, СА1В1С1 и ВА1В1С. Тогда искомое расстояние — высота ВА1В1С. Это позволит упростить чертёж и рассуждения. т.к. V(А1АВС)=V(СА1В1С1)=1/3*V(АВСА1В1С1).
С наилучшими пожеланиями, учитель-неудачник, Войкова Т.Ю.
Да, конечно, можно и таким способом решить. Спасибо.
Что значит «выразим два раза площадь треугольника MKC»?
Спасибо за вопрос. Это значит найдем площадь двумя способами.
Скажите пожалуйста, достаточно ли, в качестве пояснения на ЕГЭ этих рассуждений? Чтоб не придрались вдруг потом, решил спросить
Да.
Спасибо большое! Мои ребята используют материал Вашего сайта для самостоятельной работы. Еще раз -огромное спасибо!
Уважаемая Инна Владимировна! Спасибо за замечательный сайт! Я часто его посещаю. И всегда с пользой. Спасибо и за то, что с вами можно общаться, как это делаю я сейчас! … Под четвёртым рисунком: «Длина высоты MP треугольника и есть расстояние между прямыми AB и CB1». Объясните, пожалуйста, как такое может быть? Ведь из того, что A1B1 // AB и А1В1 и В1С лежат в одной плоскости, это не следует…
Чтобы найти расстояние между скрещивающимися прямыми, мы
1. Проводим через одну из прямых плоскость, параллельную второй прямой. В нашем случае плоскость А1В1С, содержащая прямую В1С, параллельна прямой АВ.
2. Расстояние между прямыми равно расстоянию от любой точки, лежащей на второй прямой, до полученной плоскости. В нашем случае ищем расстояние от точки М до плоскости А1В1С.
Инна Владимировна! Какова идея построения плоскости МСС1, перпендикулярной АВ? Как выбрать нужную точку и куда попадет перпендикуляр? Как найти ту прямую, где будет точка пересечения перпендикуляра с плоскостью. Видимо, для этого строили плоскость.
Наша задача построить плоскость, перпендикулярную одной из плоскостей. В нашем случае плоскости А1СВ1. Для этого мы находим прямую, лежащую в этой плоскости, которая перпендикулярна двум пересекающимся прямым плоскости МСС1 — это прямая АВ. Перпендикуляр мы опускаем из точки прямой АВ, которая лежит в перпендикулярной плоскости (то есть из М) на линию пересечения плоскостей, то есть на КС. Куда он попадет — это неважно.
Спасибо большое, еще подумаю
Можно ли использовать для решения поставленной задачи теорему-следствие из Леммы Шарыгина (и метода ортогонального проектирования), откуда расстояние между двумя скрещ.прямыми будет равно a*b/sqrt(a^2+b^2).
Где a есть длина перпендикуляра, опущенного из точки пересечения прямой m с плоскостью, в которой лежит скрещивающаяся её прямая l. А b — есть длина перпендикуляра опущенного из прямой m таким образом, что её основание есть не что иное, как точка прямой l.
Можно пользоваться любыми фактами, которые есть в учебниках.