Знаки коэффициентов квадратного трехчлена

Знаки коэффициентов квадратного трехчлена.

В этой статье я расскажу, как по графику квадратичной функции найти знаки коэффициентов квадратного трехчлена.

Чтобы определить знаки коэффициентов квадратного трехчлена по графику квадратичной функции , нужно вспомнить теорему Виета.

Согласно теореме Виета, сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение равно свободному члену.

Квадратное уравнение называется приведенным, если его старший коэффициент равен единице.

Чтобы уравнение   стало приведенным, нужно обе части уравнения разделить на старший коэффициент. Получим приведенное уравнение 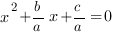. Для него справедливы соотношения:

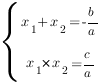
И эти же соотношения справедливы для уравнения  

По графику квадратичной функции мы легко можем определить знак коэффициента   - если ветви параболы направлены вверх, то ,  а если вниз, то .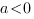

Также по графику легко определяются знаки корней (корни квадратного трехчлена 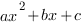  - это абсциссы точек пересечения графика функции  с осью абсцисс), а также знак корня с большим модулем.

Если оба корня положительны, то .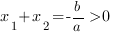

Если оба корня отрицательны, то .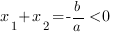

Если корень с большим модулем положителен, то .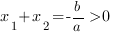

Если корень с большим модулем отрицателен, то .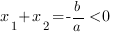

Если корни имеют одинаковые знаки, то .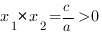

Если корни имеют разные знаки, то .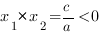

Во всех случаях, определив знак коэффициента  по направлению ветвей параболы, мы легко найдем знаки коэффициентов  и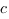

Рассмотрим примеры.

1. Определить знаки коэффициентов квадратного трехчлена 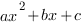, если график функции   имеет вид:

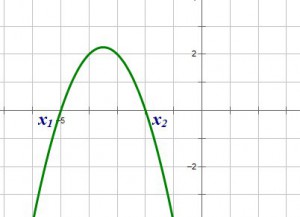
1. Ветви параболы направлены вниз, следовательно, .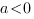

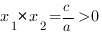
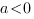
2. Корни имеют одинаковые знаки, следовательно, их произведение положительно: . Так как , следовательно, .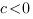

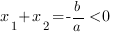
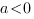
3. Оба корня отрицательны, следовательно,   их сумма отрицательна: . Так как , следовательно, .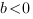

Ответ: , , .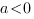

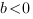
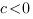
2. Определить знаки коэффициентов  квадратного трехчлена 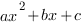, если график функции   имеет вид:

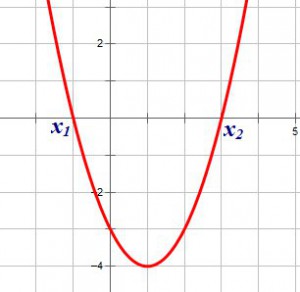
1. Ветви параболы направлены вверх, следовательно, .

2. Корни имеют разные  знаки, следовательно, их произведение отрицательно: 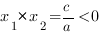. Так как , следовательно, .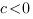

3. Корень с большим модулем положителен, следовательно,  сумма корней положительна: 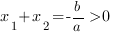. Так как , следовательно, .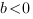

Ответ: , , .

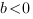
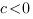
Замечание: 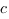- ордината точки пересечения параболы с осью , поэтому знак 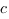можно определить сразу.