Площадь сечения — 2. Задание С2

В последнее время в вариантах для  подготовки к ЕГЭ  по математике   в Задании С2 часто стали появляться задачи на нахождение площади сечения. Рассмотрим решение такой задачи:

В прямоугольном параллелепипеде 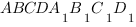 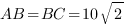,  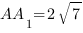. Сечение параллелепипеда проходит через точки и и 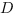образует с плоскостью угол 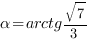.  Найдите площадь сечения.

Как мы уже видели, часто бывает удобно  находить площадь сечения через площадь его ортогональной проекции.

Нахождение площади треугольника через площадь его ортогональной проекции легко иллюстрируется таким рисунком: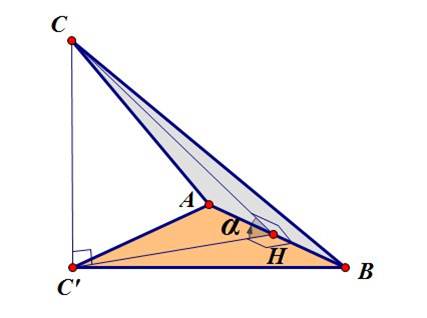 - высота треугольника , - высота треугольника , который является ортогональной проекцией треугольника . Из прямоугольного  треугольника :  .

Площадь треугольника равна .

Площадь треугольника равна .

Cледовательно,  площадь треугольника равна площади треугольника деленной на косинус угла между плоскостями треугольника и треугольника , который является ортогональной проекцией треугольника  :

Поскольку площадь любого многоугольника можно представить в виде суммы площадей треугольников, площадь многоугольника равна площади его ортогональной проекции на плоскость деленной на косинус угла между плоскостями многоугольника и его проекции.

Используем этот факт для решения задачи:

В прямоугольном параллелепипеде 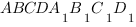 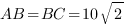 ,  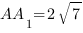.Сечение параллелепипеда проходит через точки  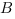и  и 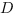образует с плоскостью  угол 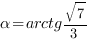.  Найдите площадь сечения.

План решения такой:

А) Строим сечение.

Б) Находим его ортогональную проекцию на плоскость основания.

В) Находим площадь ортогональной проекции.

Г) Находим площадь сечения.

Итак.

1. Сначала нам нужно построить это сечение.

Очевидно, что отрезок  принадлежит плоскости сечения и плоскости основания, то есть принадлежит линии пересечения плоскостей:

Угол между двумя плоскостями - это угол между двумя перпендикулярами, которые проведены к линии пересечения плоскостей и лежат в этих плоскостях.

. Пусть точка  - точка пересечения диагоналей основания.  - перпендикуляр к линии пересечения плоскостей, который лежит в плоскости основания:

2. Определим положение перпендикуляра, который лежит в плоскости сечения. (Помним, что если прямая перпендикулярна проекции наклонной, то она перпендикулярна и самой наклонной. Ищем наклонную по ее проекции ( ) и углу между проекцией и наклонной). Найдем тангенс угла    между  и  :

, следовательно, угол 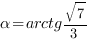 между плоскостью сечения и плоскостью основания больше, чем между     и  . То есть сечение расположено как-то так:

- точка пересечения  и 

||.

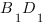Итак, вот наше сечение:

3. Найдем проекцию сечения на плоскость основания. Для этого найдем проекции точек  и .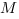

Четырехугольник  - проекция сечения  на плоскость основания. 

4. Найдем площадь четырехугольника . Для этого из площади треугольника  вычтем площадь треугольника 

Найдем площадь треугольника . Треугольник   подобен треугольнику . Найдем коэффициент подобия. Для этого рассмотрим треугольники  и :

. Следовательно,  и площадь треугольника  составляет  площади треугольника  (отношение площадей подобных фигур равно квадрату коэффициента подобия).

Тогда площадь четырехугольника  равна  площади треугольника  и равна

5. Теперь найдем .

6. И, наконец,   получаем: 

Ответ: 112

И.В. Фельдман, репетитор по математике.