В основании прямой призмы 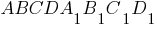 лежит квадрат
лежит квадрат  со стороной 2, а высота призмы равна
со стороной 2, а высота призмы равна  . Точка
. Точка  лежит на диагонали
лежит на диагонали  , причем
, причем  .
.
а) Постройте сечение призмы плоскостью  .
.
б) Найдите угол наклона этой плоскости к плоскости 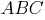 .
.

Решение.
Сначала определим где примерно расположена точка  на диагонали
на диагонали  .
.
Для этого найдем длину диагонали  .
.
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений:

отсюда 
Так как по условию  , точка
, точка  лежит чуть ниже середины диагонали
лежит чуть ниже середины диагонали  . (Точка пересечения диагоналей параллелепипеда делит их пополам.)
. (Точка пересечения диагоналей параллелепипеда делит их пополам.)

Нам нужно построить сечение призмы плоскостью  . Обозначим плоскость сечения
. Обозначим плоскость сечения  .
.
Сечение призмы плоскостью - это многоугольник, стороны которого представляют из себя линии пересечения граней призмы с секущей плоскостью.
Если две вершины многогранника, через которое нужно провести плоскость лежат в одной грани, то отрезок, соединяющий эти точки является стороной сечения. Точки  и
и  , через которые мы проводим сечение, лежат в одной грани, соединим их.
, через которые мы проводим сечение, лежат в одной грани, соединим их.
 Дальше для построения сечения воспользуемся вспомогательной плоскостью. Найдем проекции точек
Дальше для построения сечения воспользуемся вспомогательной плоскостью. Найдем проекции точек  и
и  на плоскость
на плоскость 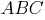 . Для этого опустим перпендикуляры из точек
. Для этого опустим перпендикуляры из точек  и
и  на плоскость
на плоскость 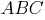 .
.

Прямые  и
и  перпендикулярны плоскости
перпендикулярны плоскости 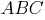 , следовательно, они параллельны:
, следовательно, они параллельны:

Через две параллельные прямые можно провести плоскость. Проведем плоскость  . Пересекающиеся прямые
. Пересекающиеся прямые  и
и  лежат в этой плоскости.
лежат в этой плоскости.

Плоскость искомого сечения  и плоскость
и плоскость  пересекаются по прямой
пересекаются по прямой  :
:

Плоскость  и плоскость основания
и плоскость основания  пересекаются по прямой
пересекаются по прямой  :
:

Пусть точка 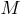 - точка пересечения прямых
- точка пересечения прямых  и
и  :
:

Точка 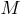 лежит и в плоскости основания, и в плоскости
лежит и в плоскости основания, и в плоскости  .
.
 ;
;
 .
.

У нас случайно получилось, что точка 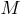 визуально лежит на ребре
визуально лежит на ребре 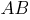 . Но, строго говоря, это не факт.
. Но, строго говоря, это не факт.
Аналогично проведем плоскость  через параллельные прямые
через параллельные прямые  и
и 
 . Пересекающиеся прямые
. Пересекающиеся прямые  и
и  лежат в этой плоскости.
лежат в этой плоскости.

Пусть точка  - точка пересечения прямых
- точка пересечения прямых  и
и  :
:

Точка  лежит и в плоскости основания, и в плоскости
лежит и в плоскости основания, и в плоскости  .
.
 ;
;
 .
.

Таким образом, точки 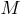 и
и  лежат и в плоскости основания, и в плоскости
лежат и в плоскости основания, и в плоскости  . Проведем через эти точки прямую
. Проведем через эти точки прямую  .
.


Найдем точки пересечения прямой  с ребрами
с ребрами 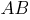 и
и 


 Теперь мы можем соединить отрезками точки
Теперь мы можем соединить отрезками точки  .
.
Итак, мы получили сечение призмы плоскостью, проходящей через точки  :
:

б) Теперь найдем угол между плоскостью сечения  и плоскостью основания.
и плоскостью основания.
Чтобы найти угол между плоскостями, нужно к линии пересечения плоскостей провести перпендикуляры, лежащие в этих плоскостях. Меньший из двух углов, образованных этими перпендикулярами, и есть угол между плоскостями.
 , так диагонали квадрата взаимно перпендикулярны.
, так диагонали квадрата взаимно перпендикулярны.
 , так как боковые ребра прямой призмы перпендикулярны плоскости основания, и, следовательно, перпендикулярны любой прямой, лежащей в плоскости основания.
, так как боковые ребра прямой призмы перпендикулярны плоскости основания, и, следовательно, перпендикулярны любой прямой, лежащей в плоскости основания.
То есть прямая  перпендикулярна двум пересекающимся прямым плоскости
перпендикулярна двум пересекающимся прямым плоскости  , и, следовательно,
, и, следовательно,  , следовательно, прямая
, следовательно, прямая  перпендикулярна любой прямой, лежащей в плоскости
перпендикулярна любой прямой, лежащей в плоскости  , в частности, прямой
, в частности, прямой 



 - так как если две параллельных плоскости пересечены третьей плоскостью, то линии пересечения этих плоскостей параллельны.
- так как если две параллельных плоскости пересечены третьей плоскостью, то линии пересечения этих плоскостей параллельны.
Поэтому 
Следовательно, угол  - угол между плоскостью
- угол между плоскостью  и плоскостью
и плоскостью 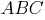
 Сделаем выносной чертеж:
Сделаем выносной чертеж:

Cделаем дополнительные построения. Проведем через точки  и
и  прямые
прямые  и
и 

и через точку  прямую
прямую  ,
, 

Рассмотрим подобные треугольники  и
и 

∠ ∠
∠
Будем искать 
1. Рассмотрим подобные треугольники  и
и 




Отсюда 
 - диагональ квадрата со стороной 2.
- диагональ квадрата со стороной 2.


Отсюда 
Тогда 
И отсюда 
Ответ: 
























При построении сечения: нельзя ли было избежать построения дополнительных плоскостей? Если провести прямую, соединяющую точку Е и середину А1С1, то эта прямая должна пересечь BD как раз в точке P. А потом проводим через P прямую, параллельную А1С1 и получаем точки M, N. И как раз получается выносной чертеж.
Можно. Но мне хотелось еще раз напомнить метод построения сечения с помощью вспомогательной плоскости — это универсальный прием.
спасибо большое!!!
Да,меня тоже поразила сложность построения сечения.16 вспомогательных чертежей к такому простому сечению.Средний ученик потеряет нить рассуждений.Но работу Вы,конечно,ведете колоссальную.
А в овете не надо ли перейти к арктангенсу? Т.е. найти именно угол?
Надо, спасибо, все время забываю)