Если в геометрической задаче присутствуют слова "внешний угол треугольника", нам надо вспомнить несколько фактов:
1. Внешним углом треугольника называется угол, смежный с каким-либо углом треугольника:
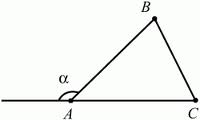
2. Сумма смежных углов равна 180°
3. Внешний угол треугольника равен сумме двух углов, не смежных с ним:

 Чтобы найти синус, косинус или тангенс внешнего угла треугольника, нужно найти эту функцию соответствующего внутреннего угла, а затем воспользоваться следующим формулами приведения:
Чтобы найти синус, косинус или тангенс внешнего угла треугольника, нужно найти эту функцию соответствующего внутреннего угла, а затем воспользоваться следующим формулами приведения:
 (1)
(1)
 (2)
(2)
 (3)
(3)
Необходимо также вспомнить, как тригонометрические функции острого угла выражаются одна через другую:




Прежде чем приступать к разбору решений задач, рекомендую вам прочитать статью о соотношении сторон и углов в прямоугольном треугольнике.
Рассмотрим решение задач из Открытого банка заданий для подготовки к ЕГЭ по математике: .
1. Задание B7 (№ 27382)
В треугольнике ABC угол C равен 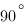 ,
,  ,
,  . Найдите тангенс внешнего угла при вершине A.
. Найдите тангенс внешнего угла при вершине A.
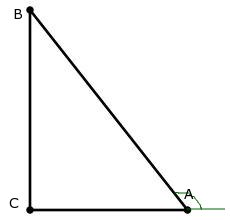 Найдем тангенс угла А, а затем воспользуемся формулой приведения.
Найдем тангенс угла А, а затем воспользуемся формулой приведения.

АС=4, ВС найдем по теореме Пифагора:

Отсюда  . Соответственно, по формуле приведения (3), тангенс внешнего угла при вершине А равен -0,25.
. Соответственно, по формуле приведения (3), тангенс внешнего угла при вершине А равен -0,25.
Ответ: -0,25
2. Задание B7 (№ 27386)
В треугольнике ABC угол C равен 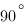 , синус внешнего угла при вершине A равен 0,1. Найдите
, синус внешнего угла при вершине A равен 0,1. Найдите  .
.
Воспользуемся формулой приведения (2): sinA=0,1
Ответ: 0,1.
3. Задание B7 (№ 27387)
В треугольнике ABC угол C равен 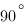 , синус внешнего угла при вершине A равен
, синус внешнего угла при вершине A равен  . Найдите
. Найдите  .
.
Найдем сначала sin A. Он равен синусу внешнего угла треугольника при вершине А. То есть  .
.
Найдем cosA c помощью основного тригонометрического тождества:

Ответ: 0,96
4. Задание B7 (№ 27389)
В треугольнике ABC угол C равен 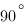 , синус внешнего угла при вершине A равен
, синус внешнего угла при вершине A равен  . Найдите
. Найдите  .
.
Найдем сначала sin A. Он равен синусу внешнего угла треугольника при вершине А. То есть  .
.
Сумма острых углов прямоугольного треугольника равна 90°, поэтому 
Ответ: 0,96
5. Задание B7 (№ 27392)
В треугольнике ABC угол C равен 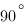 , косинус внешнего угла при вершине A равен
, косинус внешнего угла при вершине A равен  . Найдите
. Найдите  .
.
Если косинус внешнего угла при вершине A равен  , то cos A=
, то cos A= . Отсюда sinA=0,96
. Отсюда sinA=0,96
Ответ: 0,96
И.В. Фельдман, репетитор по математике.
Купить видеокурс "ВСЯ ГЕОМЕТРИЯ. Часть В"

























Хороший у вас сайт, информативный! Правда малышня моя ещё в школу не ходит.
Жаль, когда в школе учился, такого ресурса не было. 🙂 Удачи в развитии. 🙂
Почему в задании 2 ответ: -0.1 !?
Опечатка, конечно. Спасибо, исправила.
В задаче 5 в условии неверно указан знак дроби)
синус угла при основании равнобедренного треугольника равен 0,6. найдите косинус угла пр вершине этого треугольника. Помогите пожалуйста.