В этой статье я расскажу, как решать тригонометричеcкое уравнение уровня С1 для подготовки к ЕГЭ по математике:
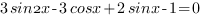
Особенность этого задания заключается в том. что в ответе необходимо указать корни, принадлежащие отрезку ![delim{[}{{-2pi};{-pi}}{]} delim{[}{{-2pi};{-pi}}{]}](http://ege-ok.ru/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_991.5_3967c8b7f3f3cd0d1c0639f145e0d55a.png)
Решим уравнение.
1.Разложим 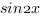 по формуле синуса двойного угла.
по формуле синуса двойного угла.
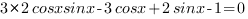
2. Сгруппируем выражение в левой части уравнения и разложим на множители.
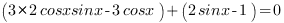

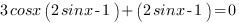
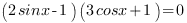
3. Приравняем каждый множитель к нулю. Получим два уравнения:
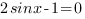 (1) или
(1) или 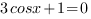 (2)
(2)
Решим уравнение (1)
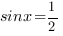
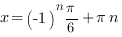 , где
, где 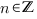
Решим уравнение (2)
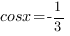
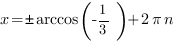 , где
, где 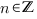
Указанному интервалу принадлежат корни 
Ответ: 
Подробное решение уравнения и выборку решений с помощью тригонометрического круга посмотрите в ВИДЕОУРОКЕ.
























спасибо все очень понятно намного лучше чем в книжки для подготовки
Да уж! Если бы в книжках так подробно и хорошо было написано, то проблем бы было меньше 🙂
Здравствуйте, Инна!
Подскажите пожалуйста, как решить это уравнение:
6\tg квадрат x + 5\tgx — 1 = 0
Заранее благодарю.
Введи замену: 1\tgx прими за y
В этом уравнении надо же приводить в общему знаменателю, потом писать ОДЗ и приравнять числитель к нулю. Как по вашему выполнить замену 1\tgx? Расскажите.
Сделать замену y=1\tgx, решить уравнение относительно y, потом вернуться к исходной переменной. Если уравнение решается с помощью замены переменной, то ОДЗ находится при возвращении к исходной переменной.
Инна Владимировна,добрый вечер!Подскажите пожалуйста с чего начать?
2sin^2x-cosx-1=0 Спасибо!
sin^2x=1-cos^2x; t=cosx
Почему вы прибавляете 2pi n при решении уравнения с косинусом..?! А к остальным просто pi n?!
Почитайте про периодичность тригонометрических функций.
Здравствуйте.
Подскажите пожалуйста какие будут решения, если tg x= -1 или tg x= -4/3 на промежутке {-3П/2;-П/2 } и как это отметить на круге?