 Отдельной темой при изучении показательных и логарифмических неравенств стоят неравенства, содержащие неизвестное в основании и в показателе степени.
Отдельной темой при изучении показательных и логарифмических неравенств стоят неравенства, содержащие неизвестное в основании и в показателе степени.
В этой статье мы изучим пошаговый алгоритм решения неравенств, которые назовем "особые логарифмические неравенства", хотя их, с тем же успехом, можно отнести к "особым показательным неравенствам".
Рассмотрим решение неравенств вида:


Как мы знаем, переход в показательном неравенстве от степеней к показателям степеней зависит от основания степени:
если основание степени больше единицы, то при переходе к выражениям, стоящим в показателе, знак неравенства сохраняется
если основание степени больше нуля, но меньше единицы, то при переходе к выражениям, стоящим в показателе, знак неравенства меняется на противоположный.
Поскольку наше неравенство не совсем показательное: основание нашей степени зависит от х, рассмотрим отдельно случаи, когда  и
и  . В этих случаях нам надо найти, при каких значениях х выполняются эти условия, а затем проверить, верно ли наше неравенство при этих значениях неизвестного.
. В этих случаях нам надо найти, при каких значениях х выполняются эти условия, а затем проверить, верно ли наше неравенство при этих значениях неизвестного.
Нужно обратить внимание на то, что если в основании степени стоит ноль, то показатель степени должен быть положительным.
В общем виде мы получим совокупность четырех систем неравенств:








На практике неравенства c неизвестным в основании и в показателе степени удобно решать по такому алгоритму:
1. Рассматриваем отдельно два случая, когда основания степеней равны 0 или 1. Найдем, при каких значении х выполняются эти условия и проверим, верно ли наше неравенство при этих значениях х. Следим за тем, чтобы у степени, в основании которой стоит ноль, показатель был положительным.
2. Записываем правую часть неравенства в виде степени с тем же основанием, что и в левой части.
3. Рассматриваем еще два случая, когда основания степеней принимают значения больше ноля или от ноля до единицы.
Давайте рассмотрим пример решения неравенства такого типа.
Решим неравенство:

Запишем системы, которые у нас получатся:
1. 

2. 

3. 

4. 

Запишем решения каждой системы:
1) 
2) 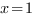
3) 
4)  (
(![{delim{(}{1;2}{]}} {delim{(}{1;2}{]}}](http://ege-ok.ru/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_991.5_3c340fdf41fd5647436351084587a222.png)
Объединим все решения: ![{x}in{delim{[}{0;2}{]}} {x}in{delim{[}{0;2}{]}}](http://ege-ok.ru/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_991.5_45cf10476151e71b7f8c5655e5481630.png)
Ответ: ![{x}in{delim{[}{0;2}{]}} {x}in{delim{[}{0;2}{]}}](http://ege-ok.ru/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_991.5_45cf10476151e71b7f8c5655e5481630.png)
Предлагаю вам посмотреть ВИДЕОУРОК с подробным решением неравенства уровня С3:


























На 10:00 минуте видео вы записали 0<x<9. Мне кажется, что правильней было записать -1<x<9. Поправьте меня, если я ошибся.
Да, конечно, это очевидная опечатка: -1