Сайт репетитора по математике Фельдман Инны Владимировны. Профессиональные услуги репетитора по математике в Москве. Подготовка к ГИА и ЕГЭ, помощь отстающим.
14 Апр 2014
12 Задание (2022) (C1)ТРИГОНОМЕТРИЯУРАВНЕНИЯ И НЕРАВЕНСТВА С МОДУЛЕМ

Тригонометрическое уравнение с модулем

Решим тригонометрическое уравнение с модулем:

cos{3x}+delim{|}{cos{x}}{|}=sin{2x}

Так как уравнение содержит модуль, нам нужно этот модуль раскрыть по определению модуля.

Рассмотри два случая:

а) cos{x}>=0 -  в этом случае модуль раскрываем с тем же знаком.

б) cos{x}<0 -  в этом случае модуль раскрываем с противоположным  знаком.

Итак.

а) cos{x}>=0

Раскрываем модуль с тем же знаком и получаем уравнение

cos{3x}+cos{x}=sin{2x}

Представим сумму косинусов в виде произведения, а правую часть уравнения разложим по формуле синуса двойного угла.

2cos{{3x+x}/2}cos{{3x-x}/2}=2sin{x}cos{x}

2cos{2x}cos{x}=2sin{x}cos{x}

Перенесем все влево и вынесем за скобки 2cos{x}

2cos{2x}cos{x}-2sin{x}cos{x}=0

2cos{x}(cos{2x}-sin{x})=0

Отсюда cos{x}=0 или cos{2x}-sin{x}=0

cos{x}=0 при x={pi}/2+{pi}n,~n{in}{bbZ}

Решим второе уравнение: cos{2x}-sin{x}=0

1-2sin^2{x}-sin{x}=0

Введем замену переменной: sin{x}=t, ~~delim{|}{t}{|}<=1

Решим квадратное уравнение относительно 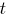t:

1-2t^2-t=0

Умножим на -1:

2t^2+t-1=0

t_1=-1;~~t_2=1/2

Отсюда sin {x}=-1 или sin {x}=1/2

x=-{pi}/2+2{pi}n,~n{in}{bbZ}

x={pi}/6+2{pi}n,~n{in}{bbZ}

x={5{pi}}/6+2{pi}n,~n{in}{bbZ}

Нанесем все решения на тригонометрический круг и вспомним, что полученное уравнение "действительно" только при cos{x}>=0, то есть в первой и четвертой четвертях:

Итак, если cos{x}>=0, корни уравнения

x={pi}/6+2{pi}n,~n{in}{bbZ} и x={pi}/2+{pi}n,~n{in}{bbZ}

Рассмотрим второй случай:

б) cos{x}<0

В этом случае, так как подмодульное выражение отрицательно, раскрываем модуль с противоположным знаком:

cos{3x}-cos{x}=sin{2x}

Разность косинусов представим в виде произведения.

-2sin{{3x-x}/2}sin{{3x+x}/2}=sin{2x}

-2sin{x}sin{2x}-sin{2x}=0

Вынесем за скобки -sin{2x}. Получим:

-sin{2x}(2sin{x}+1)=0

Отсюда sin{2x}=0;~~2x={pi}n,~n{in}{bbZ}; x={{pi}/2}n,~n{in}{bbZ}

или sin{x}=-1/2

x=-{pi}/6+2{pi}n,~n{in}{bbZ}

x=-{5{pi}}/6+2{pi}n,~n{in}{bbZ}

Нанесем корни на тригонометрический круг и отберем те значения, при которых выполняется условие cos{x}<0:

Получим решения:

x={pi}+2{pi}n,~n{in}{bbZ}

x=-{5{pi}}/6+2{pi}n,~n{in}{bbZ}

Объединим оба случая и получим окончательный

Ответ: x={pi}/6+2{pi}n,~n{in}{bbZ}

x={pi}/2+{pi}n,~n{in}{bbZ}

x={pi}+2{pi}n,~n{in}{bbZ}

x=-{5{pi}}/6+2{pi}n,~n{in}{bbZ}

Можно объединить первую и последнюю серии решений, и тогда получим такой

Ответ: x={pi}/6+{pi}n,~n{in}{bbZ}

x={pi}/2+{pi}n,~n{in}{bbZ}

x={pi}+2{pi}n,~n{in}{bbZ}

И.В. Фельдман, репетитор по математике.

Для вас другие записи этой рубрики:

Тригонометрическое уравнение с модулем
| Отзывов (5)

Отзывов (5)

  1. Елена
    в 12:19

    Мне ну о-о-чень нравится!
    Ответить
  2. Эля
    в 12:15

    Можно узнать, почему в ответе при решении 2го случая получили х=П+2Пn, если при решении такого не было?
    Ответить
    • Инна
      в 15:14

      Это часть решения {{pi}/2}n, которая удовлетворяет условию cosx<0
      Ответить
  3. Наталия
    в 17:52

    В первом случае sinx=-1 опечатка.
    Ответить
  4. Robert
    в 10:00

    страшно
    Ответить

Добавить комментарий

Ваш e-mail не будет опубликован. Обязательные поля помечены *