
Решение простейших тригонометрических уравнений.
Решение тригонометрических уравнений любого уровня сложности в конечном итоге сводится к решению простейших тригонометрических уравнений. И в этом наилучшим помощником снова оказывается тригонометрический круг.
Вспомним определения косинуса и синуса.
Косинусом угла ![]() называется абсцисса (то есть координата по оси
называется абсцисса (то есть координата по оси ![]() ) точки на единичной окружности, соответствующей повороту на данный угол
) точки на единичной окружности, соответствующей повороту на данный угол ![]() .
.
Синусом угла ![]() называется ордината (то есть координата по оси
называется ордината (то есть координата по оси ![]() ) точки на единичной окружности, соответствующей повороту на данный угол
) точки на единичной окружности, соответствующей повороту на данный угол ![]() .
.
Положительным направлением движения по тригонометрическому кругу считается движение против часовой стрелки. Повороту на 0 градусов ( или 0 радиан) соответствует точка с координатами (1;0)
Используем эти определения для решения простейших тригонометрических уравнений.
1. Решим уравнение ![]()
Этому уравнению удовлетворяют все такие значения угла поворота ![]() , которые соответствуют точкам окружности, ордината которых равна
, которые соответствуют точкам окружности, ордината которых равна ![]() .
.
Отметим на оси ординат точку с ординатой ![]() :
:
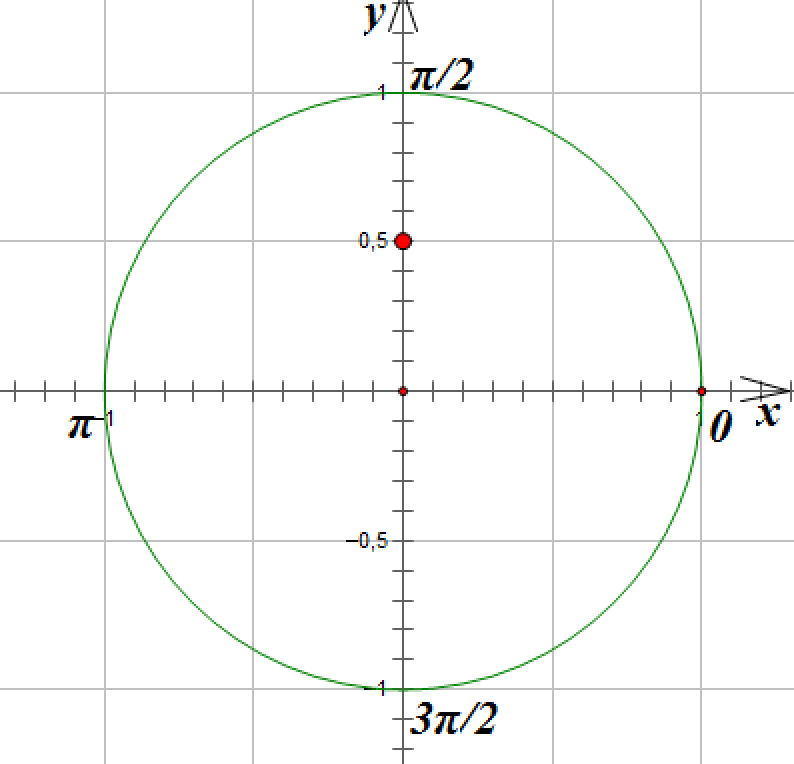
Проведем горизонтальную линию параллельно оси абсцисс до пересечения с окружностью. Мы получим две точки, лежащие на окружности и имеющие ординату![]() . Эти точки соответствуют углам поворота на
. Эти точки соответствуют углам поворота на ![]() и
и![]() радиан:
радиан:
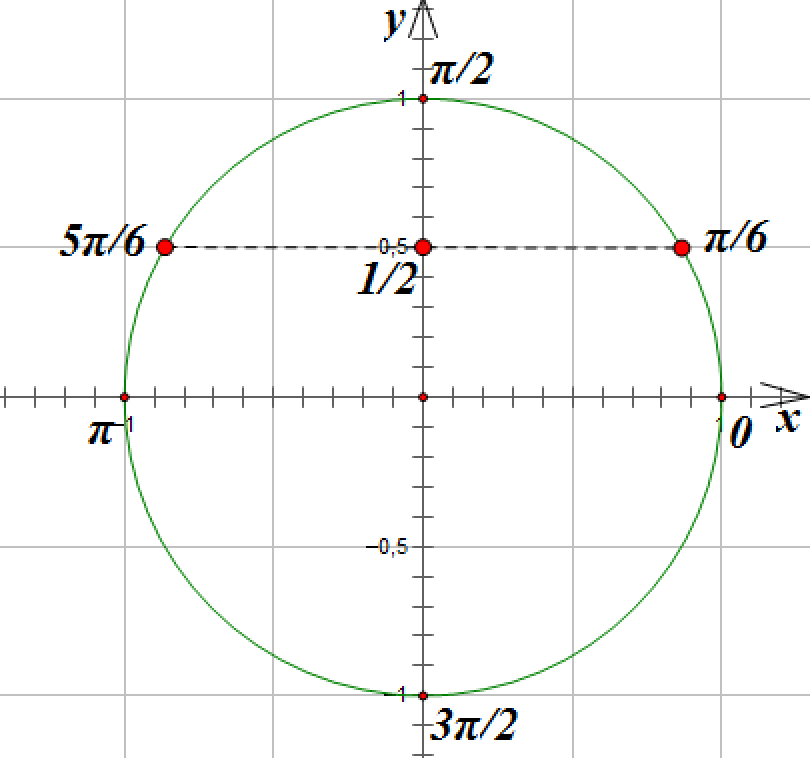
Если мы, выйдя из точки, соответствующей углу поворота на ![]() радиан, обойдем полный круг, то мы придем в точку, соответствующую углу поворота на
радиан, обойдем полный круг, то мы придем в точку, соответствующую углу поворота на ![]() радиан и имеющую ту же ординату. То есть этот угол поворота также удовлетворяет нашему уравнению. Мы можем делать сколько угодно "холостых" оборотов, возвращаясь в ту же точку, и все эти значения углов будут удовлетворять нашему уравнению. Число "холостых" оборотов обозначим буквой
радиан и имеющую ту же ординату. То есть этот угол поворота также удовлетворяет нашему уравнению. Мы можем делать сколько угодно "холостых" оборотов, возвращаясь в ту же точку, и все эти значения углов будут удовлетворять нашему уравнению. Число "холостых" оборотов обозначим буквой ![]() (или
(или ![]() ). Так как мы можем совершать эти обороты как в положительном, так и в отрицательном направлении,
). Так как мы можем совершать эти обороты как в положительном, так и в отрицательном направлении,![]() (или
(или ![]() ) могут принимать любые целые значения.
) могут принимать любые целые значения.
То есть первая серия решений исходного уравнения имеет вид:
![]() ,
, ![]() ,
, ![]() - множество целых чисел (1)
- множество целых чисел (1)
Аналогично, вторая серия решений имеет вид:
![]() , где
, где ![]() ,
, ![]() . (2)
. (2)
Как вы догадались, в основе этой серии решений лежит точка окружности, соответствующая углу поворота на ![]() .
.
Эти две серии решений можно объединить в одну запись:
![]()
Если мы в этой записи возьмем ![]() ( то есть четное
( то есть четное ![]() ), то мы получим первую серию решений.
), то мы получим первую серию решений.
Если мы в этой записи возьмем ![]() ( то есть нечетное
( то есть нечетное ![]() ), то мы получим вторую серию решений.
), то мы получим вторую серию решений.
2. Теперь давайте решим уравнение ![]()
Так как ![]() - это абсцисса точки единичной окружности, полученной поворотом на угол
- это абсцисса точки единичной окружности, полученной поворотом на угол ![]() , отметим на оси
, отметим на оси ![]() точку с абсциссой
точку с абсциссой ![]() :
:
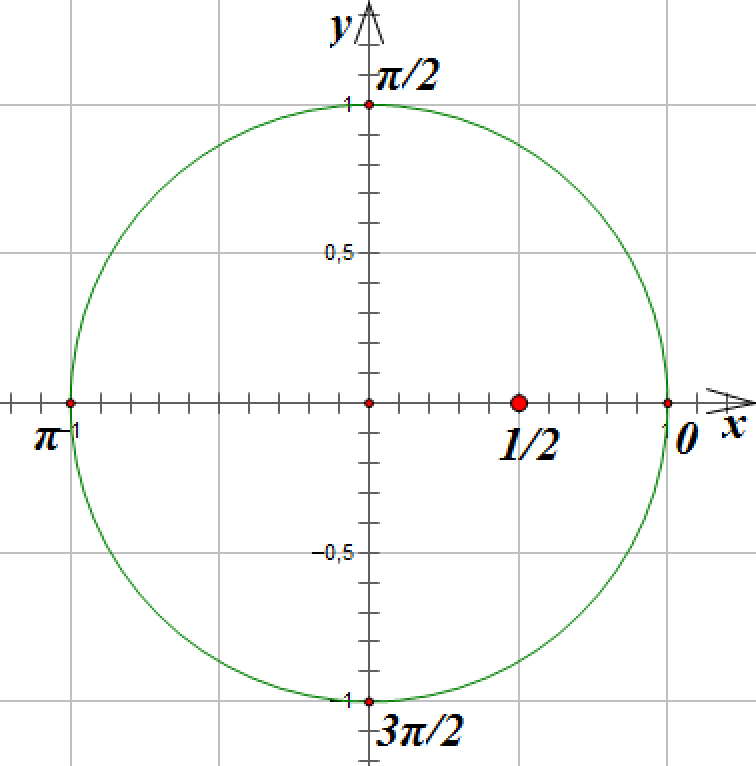
Проведем вертикальную линию параллельно оси ![]() до пересечения с окружностью. Мы получим две точки, лежащие на окружности и имеющие абсциссу
до пересечения с окружностью. Мы получим две точки, лежащие на окружности и имеющие абсциссу ![]() . Эти точки соответствуют углам поворота на
. Эти точки соответствуют углам поворота на ![]() и
и![]() радиан. Вспомним, что при движении по часовой стрелки мы получаем отрицательный угол поворота:
радиан. Вспомним, что при движении по часовой стрелки мы получаем отрицательный угол поворота:
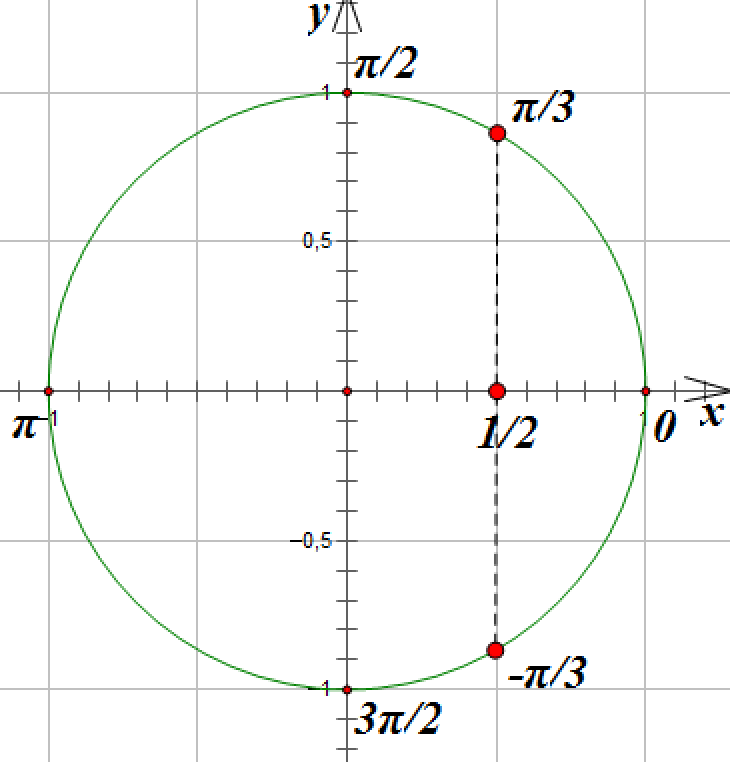
Запишем две серии решений:
![]() ,
, ![]()
![]() ,
, ![]()
(Мы попадаем в нужную точку, пройдя из основной полный круг, то есть ![]() .
.
Объедим эти две серии в одну запись:
![]()
3. Решим уравнение ![]()
Линия тангенсов проходит через точку с координатами (1,0) единичной окружности параллельно оси OY
Отметим на ней точку, с ординатой равной 1 (мы ищем, тангенс каких углов равен 1):
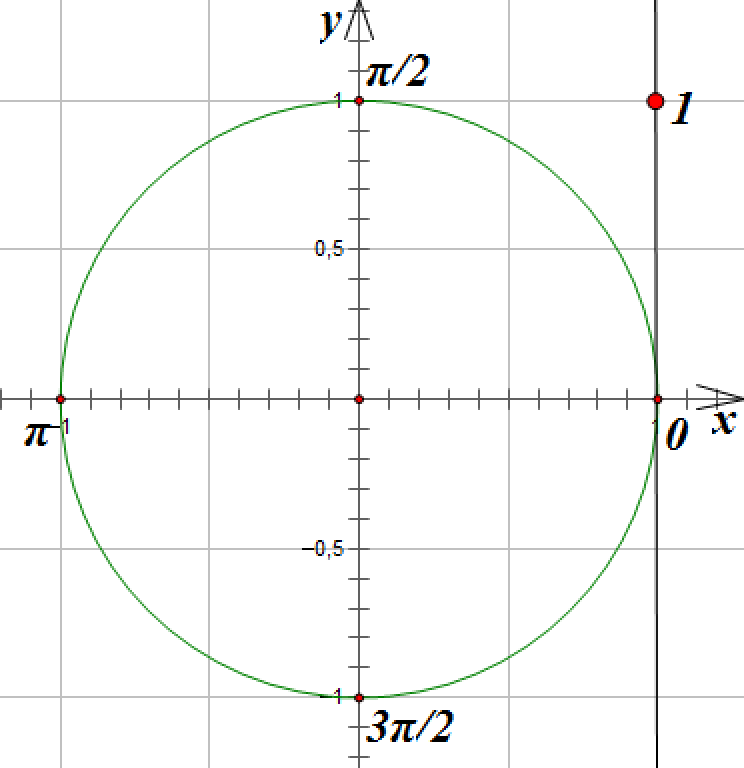
Соединим эту точку с началом координат прямой линией и отметим точки пересечения прямой с единичной окружностью. Точки пересечения прямой и окружности соответствуют углам поворота на ![]() и
и ![]() :
:
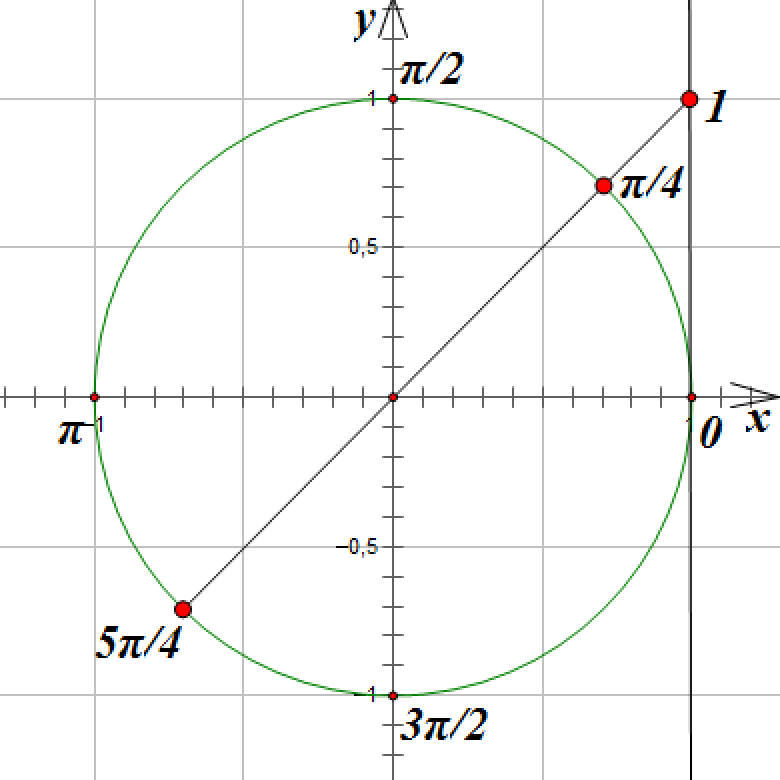
Так как точки, соответствующие углам поворота, которые удовлетворяют нашему уравнению, лежат на расстоянии ![]() радиан друг от друга, то мы можем записать решение таким образом:
радиан друг от друга, то мы можем записать решение таким образом:
![]() ,
, ![]()
4. Решим уравнение ![]()
Линия котангенсов проходит через точку с координатами ![]() единичной окружности параллельно оси
единичной окружности параллельно оси ![]() .
.
Отметим на линии котангенсов точку с абсциссой -1:
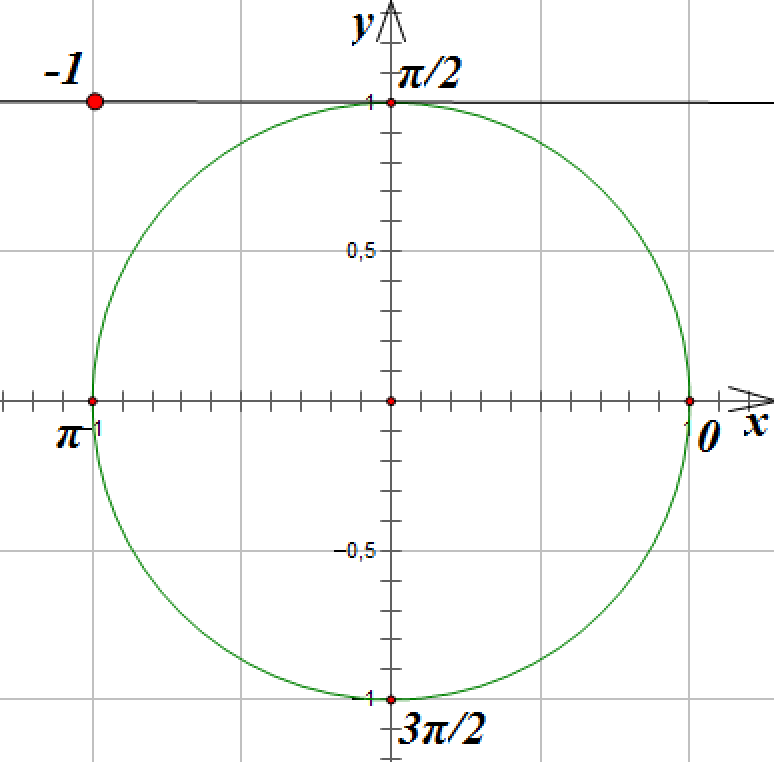
Соединим эту точку с началом координат прямой и продолжим ее до пересечения с окружностью. Эта прямая пересечет окружность в точках, соответствующих углам поворота на![]() и
и ![]() радиан:
радиан:
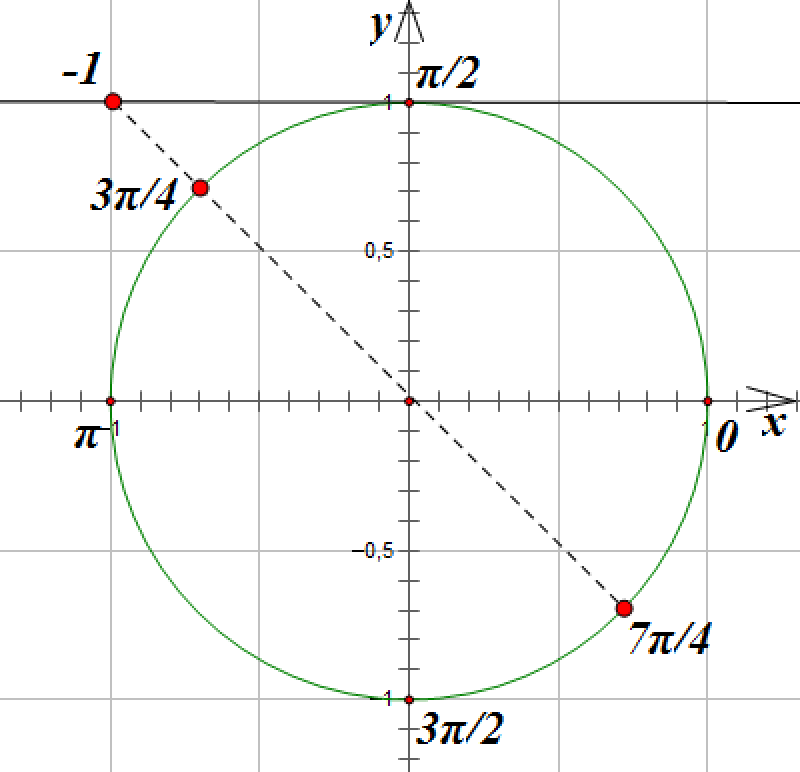
Поскольку эти точки отстоят друг от друга на расстояние, равное ![]() , то общее решение этого уравнения мы можем записать так:
, то общее решение этого уравнения мы можем записать так:
![]()
В приведенных примерах, иллюстрирующих решение простейших тригонометрических уравнений были использованы табличные значения тригонометрических функций.
Однако, если в правой части уравнения стоит не табличное значение, то мы в общее решение уравнения подставляем значение обратной тригонометрической функции:
![]()
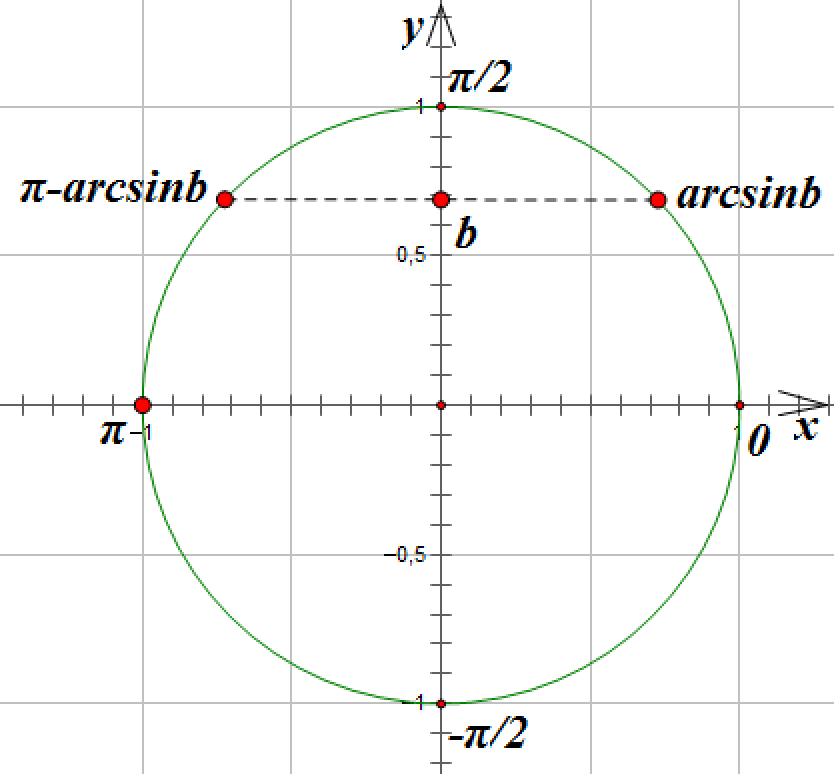
![]()
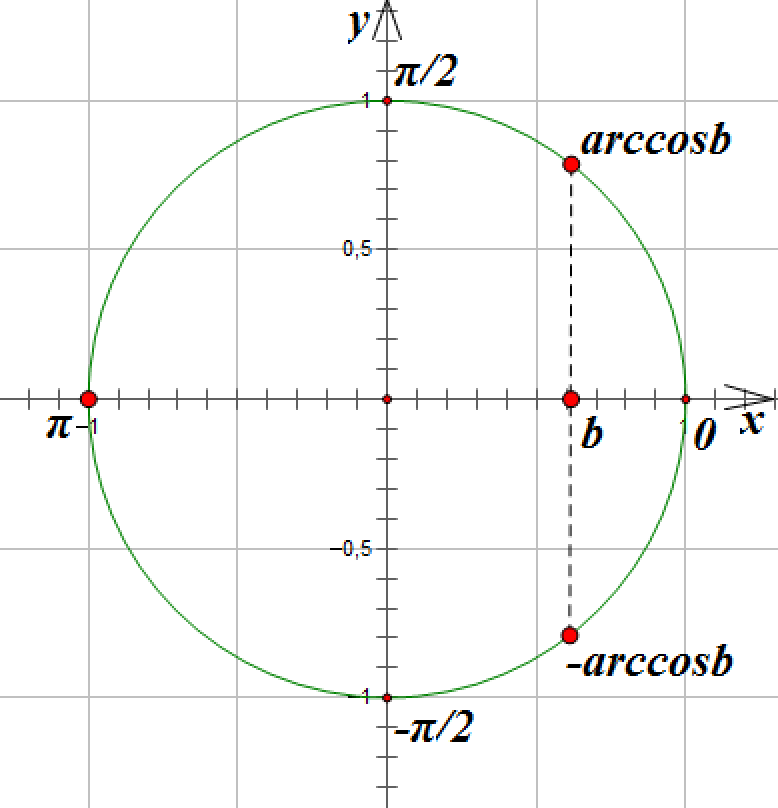
![]()
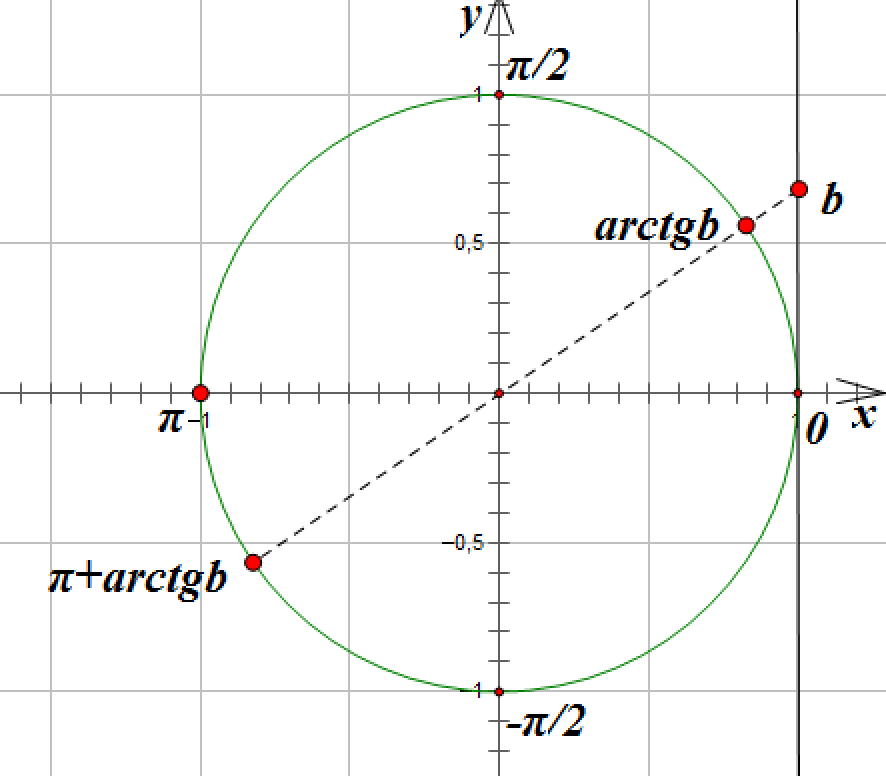
![]()
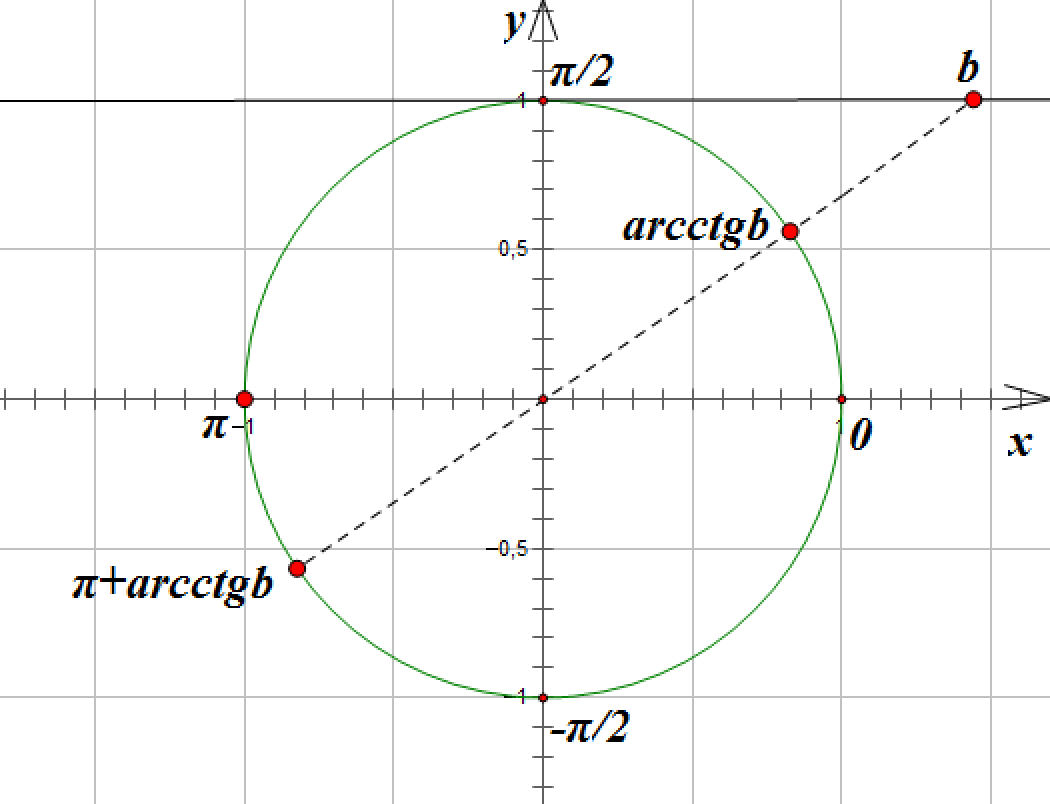
ОСОБЫЕ РЕШЕНИЯ:
1 ![]()
Отметим на окружности точки, ордината которых равна 0:
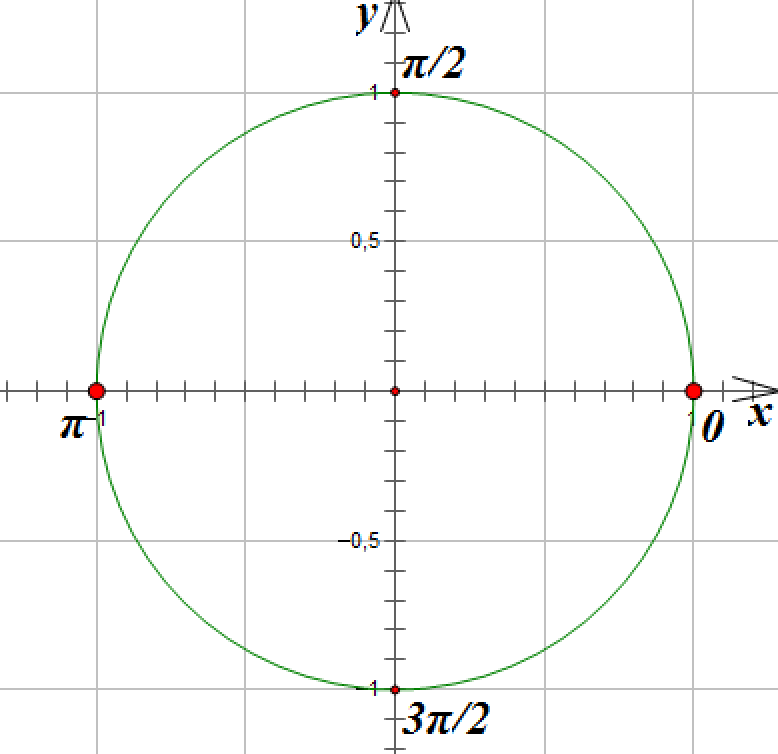
![]()
2. ![]()
Отметим на окружности единственную точку, ордината которой равна 1:
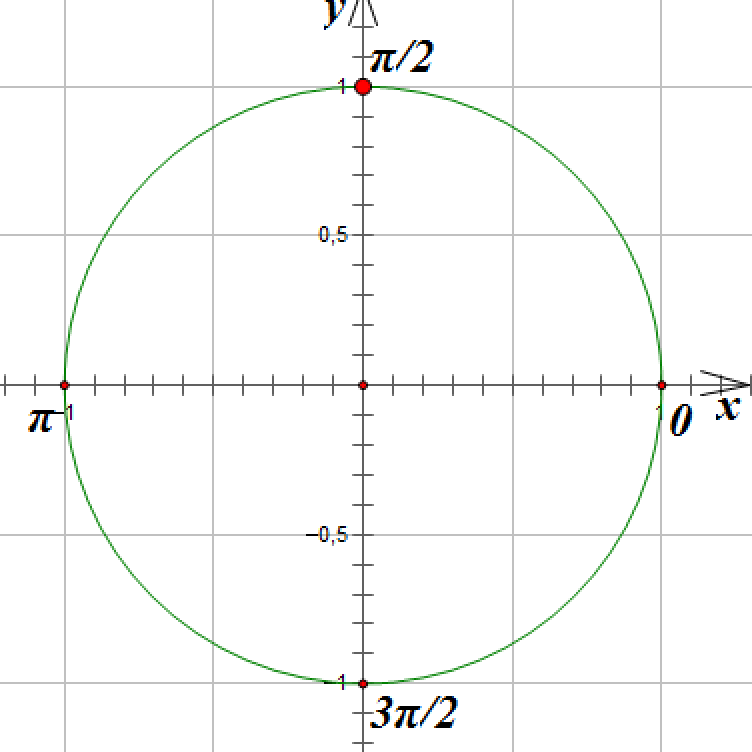
![]()
3. ![]()
Отметим на окружности единственную точку, ордината которой равна -1:
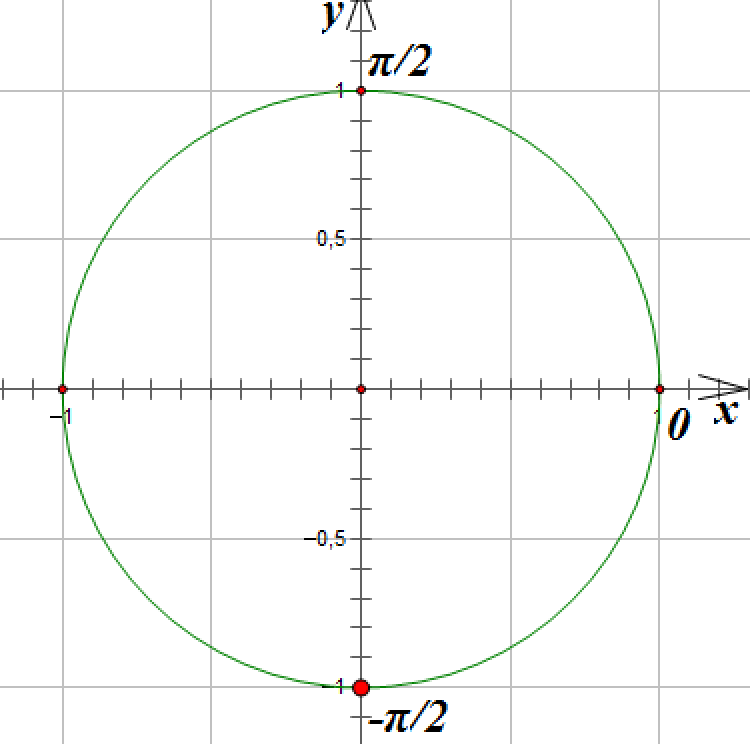
Так как принято указывать значения, наиболее близкие у нулю, решение запишем так: ![]()
4. ![]()
Отметим на окружности точки, абсцисса которых равна 0:
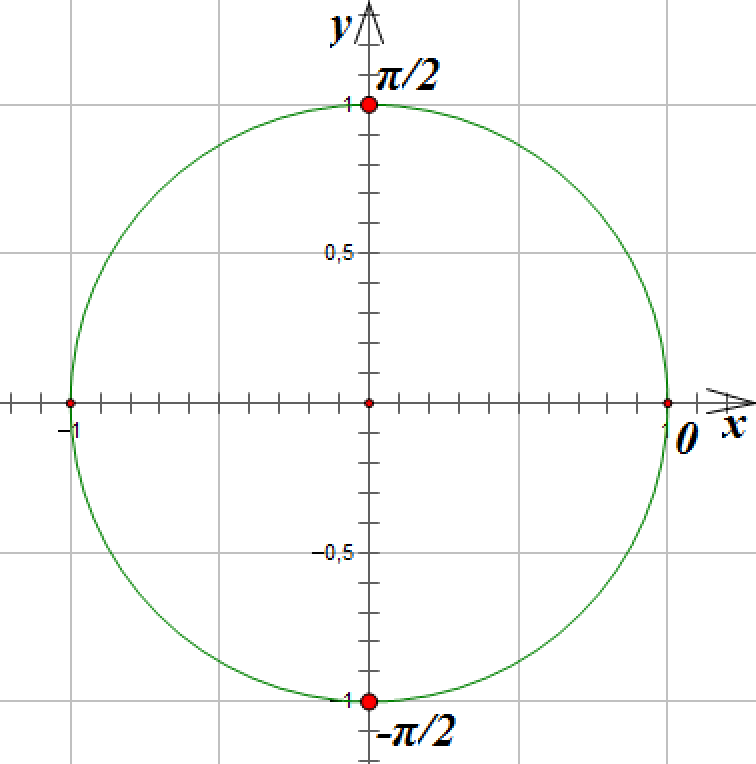
![]()
5. ![]()
Отметим на окружности единственную точку, абсцисса которой равна 1:
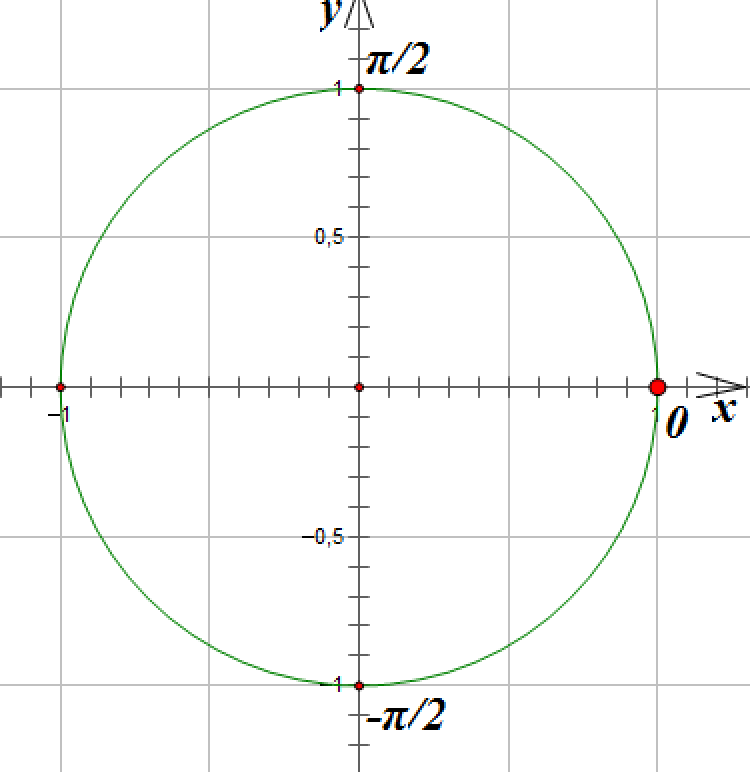
![]()
6. ![]()
Отметим на окружности единственную точку, абсцисса которой равна -1:
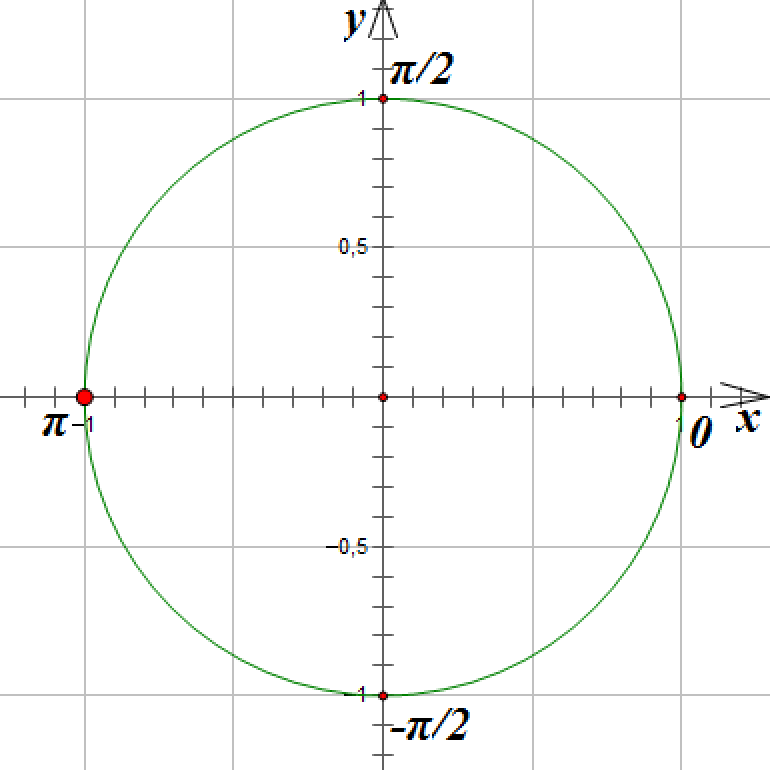
![]()
И чуть более сложные примеры:
1. ![]()
Синус равен единице, если аргумент равен ![]()
Аргумент у нашего синуса равен ![]() , поэтому получим:
, поэтому получим:
![]() . Разделим обе части равенства на 3:
. Разделим обе части равенства на 3:
![]()
Ответ: ![]()
2. ![]()
Косинус равен нулю, если аргумент косинуса равен ![]()
Аргумент у нашего косинуса равен ![]() , поэтому получим:
, поэтому получим:
![]()
Выразим ![]() , для этого сначала перенесем
, для этого сначала перенесем ![]() вправо с противоположным знаком:
вправо с противоположным знаком:
![]()
Упростим правую часть:
![]()
Разделим обе части на -2:
![]()
Заметим, что перед слагаемым ![]() знак не меняется, поскольку k может принимать любые целые значения.
знак не меняется, поскольку k может принимать любые целые значения.
Ответ: ![]()
И в заключение посмотрите видеоурок "Отбор корней в тригонометрическом уравнении с помощью тригонометрической окружности"
На этом разговор о решении простейших тригонометрических уравнений мы закончим. Следующий раз мы с вами поговорим о том, как решать простейшие тригонометрические неравенства.
























помогите пожалуйста)
Здравствуйте!
Помогите пожалуйста графически решить тригонометрические уравнения
а) ctgx=sqrt3/2 б) ctgx=0
Подскажите пожалуйста верно ли решено:
Sin(2x)=1/2
x=(-1)^n*pi/12+(pi/2)*n
В другом представлении:
x1=pi/12+pi*n
x2=11pi/12+pi*n (в одном источнике почему-то 5pi/12+pi*n, не понимаю)
И еще вопрос. Если требуется изобразить множество решений уравнения на числовой окружности, то в данном случае следует отметить точки pi/12 и 11pi/12?
Спасибо.
Sin(2x)=1/2
2x=π/6+2πn, x=π/12+πn
или
2x=5π/6+2πn, x=5π/12+πn
Помогите, пожалуйста я не могу решить сама задание «найдите корни уравнения cosx=-1/2 принадлежащее отрезку [-2π;3π]заранее спасибо!!!
Корни уравнения:
 в положительном направлении и записываем корни:
в положительном направлении и записываем корни: 
Теперь идем по тригонометрическому кругу от точки
см: //ege-ok.ru/wp-content/uploads/2016/01/1.png
Инна Владимировна! У меня аналогичное задание: определить корни на промежутке. Пытаюсь разобрать Решение уравнения Инны. Поясните, пожалуйста, как Вы выбрали нужные корни? Заранее спасибо!
Жанна, если вы совсем не умеете отбирать корни, то лучше вам купить видеолекцию: Видеолекция 22 «Введение в тригонометрию. Решение всех типов тригонометрических уравнений с выборкой решений»
цена 290 руб. Я вышлю ссылки после оплаты. Как оплатить см. здесь: //ege-ok.ru/2012/12/03/sposobyi-oplatyi
укажите наибольшее и наименьшее значение выражения 4+cos a(альфа)
Наименьшее значение 3, наибольшее 5
Здравствуйте! При решении уравнения sin^2(x)=(корень3)/2 каким образом нужно объединять корни?
Писать ±π/3+πk или π/3+πk/2 ?
Уравнение ?
?
Да.
Проверьте условие.
Прошу прощения, уравнение sin^2x=3/4!
Тогда ±π/3+πk. π/3+πk/2 — совсем другие точки.
Спасибо. А в уравнении sin^2x=1/2 аналогично ответ будет ±π/4+πk? В сборнике ФИПИ указан ответ π/4+πk/2, а у меня получается ±π/4+πk.
Да. В последнем уравнении оба ответа верны — нанесите на тригонометрический круг и посмотрите. Расстояние между точками в решении ±π/4+πk равно π/2, поэтому можно решение записать как π/4+πk/2. А в предыдущем уравнении это нет так.
Всё понятно, спасибо большое!