Расстояние между двумя прямыми. Метод координат. Задание 14
В этой статье я хочу показать решение задачи на нахождение расстояния между скрещивающимися прямыми, которую мы уже решали геометрическим способом, но теперь с помощью метода координат. Я специально показываю решение одной задачи разными способами, чтобы у вас была возможность выбрать наиболее удобный для вас.
Итак, аналитический способ решения задачи:
В правильной треугольной призме 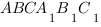 , все ребра которой равны 1, найдите расстояние между прямыми
, все ребра которой равны 1, найдите расстояние между прямыми  и
и 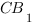 :
:
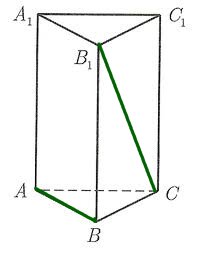 Как мы помним из геометрического метода решения этой задачи, расстояние между прямыми
Как мы помним из геометрического метода решения этой задачи, расстояние между прямыми  и
и 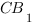 есть расстояние от точки
есть расстояние от точки 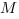 , которая является серединой отрезка
, которая является серединой отрезка  до плоскости
до плоскости 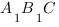 :
:

Рассстояние 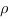 от точки
от точки 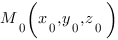 до плоскости
до плоскости  вычисляется по такой формуле:
вычисляется по такой формуле:
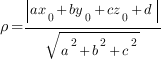
Поместим нашу призму в систему координат. Если мы решаем задачу с кубом или прямоугольным параллелепипедом, то выбор системы координат очевиден: мы помещаем начало координат в одну из вершин куба, а оси направляем вдоль ребер. В случае призмы это не столь очевидно.
Нам надо выбрать систему координат таким образом, чтобы координаты точки 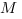 и точек
и точек 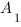 ,
, 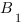 и
и  , задающих плоскость
, задающих плоскость  вычислялись наиболее простым способом и содержали как можно больше нулей. Поэтому удобно выбрать систему координат вот таким образом:
вычислялись наиболее простым способом и содержали как можно больше нулей. Поэтому удобно выбрать систему координат вот таким образом:
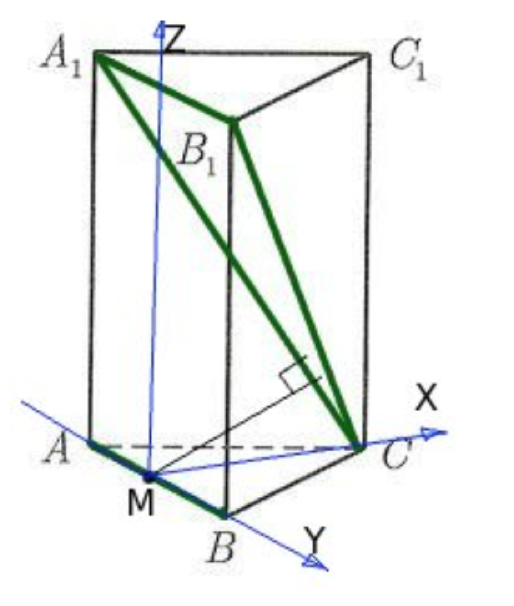
Запишем координаты нужных нам точек:
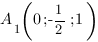
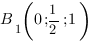
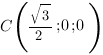
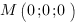
Чтобы найти коэффициенты  ,
,  ,
, 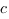 и
и 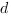 в уравнении
в уравнении  плоскости
плоскости 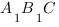 , примем коэффициент
, примем коэффициент 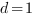 , и подставим координаты точек
, и подставим координаты точек 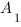 ,
, 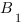 и
и 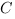 в уравнение плоскости. (Мы приняли коэффициент
в уравнение плоскости. (Мы приняли коэффициент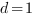 , так как наша плоскость не проходит через начало координат.)
, так как наша плоскость не проходит через начало координат.)
Получим систему уравнений:
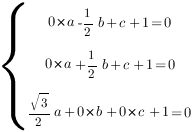
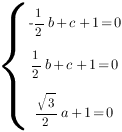
Отсюда:
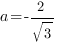 ,
,
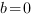 ,
,
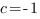
Подставим значения коэффициентов и координаты точки 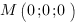 в формулу для расстояния. Получим:
в формулу для расстояния. Получим:
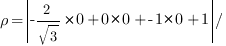
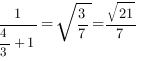
Ответ: 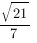

























Спасибо. Очень познавательно.