Задача на подобие и теорема Менелая. Задание 16
Хочу вам предложить два способа решения одной интересной задачи. Первый способ довольно длинный, но его нужно знать, поскольку прием, который в нем используется, применяется довольно часто при решении задач, в которых дано отношение отрезков.
Второй способ позволяет решить задачу в одно действие, но в нем используется Теорема Менелая, которую обычно в школе не проходят. Поэтому нужно будет с этой теоремой познакомиться.
Итак задача:
На сторонах AB и BC треугольника ABC взяты соответственно точки M и N так, что AM:MB=2:3, BN:NC=2:1. Отрезки AN и CM пересекаются в точке O. Найти отношение CO:OM.
Вот наш треугольник:
Проведем через точку В прямую параллельно отрезку AB, затем продолжим отрезок AN до пересечения с этой прямой и поставим там точку К:
Рассмотрим треугольники ANC и BNK. Эти треугольники подобны, так как AC||BK. Стороны треугольника BNK относятся к сторонам треугольника ANC как 2:1.
Пусть AC=x, BK=2x.
Теперь продолжим отрезок MC до пересечения с прямой BK. Поставим там точку L.
Мы получили подобные треугольники LMB и AMC, сходственные стороны которых относятся как 3:2. Так как AC=x, то LB=1,5x.
Пусть LM=3n, MC=2n. Тогда LC=5n.
Теперь рассмотрим подобные треугольники LOK и AOC.
, следовательно, 
. Пусть LO=3,5z, OC=z. Тогда LO+OC=LC=4,5z.
Получили, что 5n=4,5z. Тогда MC=2n=
z. Отсюда MO=MC-CO=z-z=
z
Отсюда CO:OM=z:z=5:4=1,25.
Ответ: 1,25
Теперь обещанная теорема Менелая. Я не буду ее доказывать, поскольку доказательство можно найти в интернете. Покажу, как она используется в этой задаче.
ТЕОРЕМА МЕНЕЛАЯ
Пусть прямая пересекает треугольник ABC, причем 
– точка ее пересечения со стороной AB,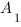 
– точка ее пересечения со стороной BC, и 
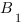– точка ее пересечения с продолжением стороны AC. Тогда
Мы начинаем обход треугольника из какой-либо вершины в произвольном направлении. В числителе каждая дроби - расстояние от вершины треугольника до точки пересечения прямой со стороной треугольника или ее продолжением, в знаменателе - расстояние от точки пересечения до следующей вершины.
Применим эту теорему к нашей задаче. Рассмотрим треугольник MBC и прямую AN:
Запишем теорему Менелая для этого треугольника:
Ответ: 1,25
И.В. Фельдман, репетитор по математике
Очень красивое решение!
1. В плоскости двух параллельных прямых а и b дана точка С,не принадлежащая этим прямым.Через нее проведена прямая с.Найти все возможные расположения прямой c относительно прямых а и b.
2.Сторона KM треугольника KLM параллельна плоскости альфа.Точки G
и H принадлежат соответственно его сторонам KL и KM.Точка P-точка пересечения прямой GH с плоскостью альфа.Постройте точки пересечения прямых KL и LM с плоскостью альфа.Найдите линию пересечения плоскостей треугольника KLM и плоскости альфа.
3.Прямая b параллельна плоскости бета.Определите положение данной прямой относительно прямых а)лежащих в плоскости бета.б)параллельных плоскости бета.в)пересекающих плоскость бета.
Помогите пожалуйста решить контрольную!Заранее благодарю.
И хорошо, что тебе никто не подсказал, двоечница.
Теоремы Менелая нет в курсе, зато есть вектора — решение получается короткое и красивое
Буду вам благодарна, если вы приведете свое решение через вектора.
Прием деления отрезка в заданном отношении — как при вычислении длины биссектрисы. Введем вектора СВ=а СА=b и обозначим отношение отрезков AO:ON=beta:1 CO:OM=alfa:1. Надо найти alfa.
из ABC: CM=2/5a+3/5b CO=alfa/(alfa+1)CM=…
С другой стороны,
из ANC: CO=beta/(beta+1)a/3 + 1/(beta+1)b
Приравнивая к-ты разложения вектора CO, получим линейную систему относительно alfa и beta и найдем alfa.
Спасибо!