Решение семи типов рациональных уравнений четвертой степени, сводящихся к квадратным, мы рассматривали здесь. Однако, далеко не всегда тип уравнения очевиден.
Рассмотрим решение вот такого уравнения:
Очевидно, что перемножать скобки смысла не имеет.
Мы видим, что квадратные трехчлены во второй и третьей скобках можно легко разложить на множители. Сделаем это. (Помним: если не знаешь что делать, раскладывай на множители).
Это уравнение некоторым образом напоминает уравнение первого типа.
Сгруппируем последние две скобки по две так, чтобы суммы коэффициентов были равны:
Перемножим их попарно.
Теперь замена переменной становится очевидной. Обозначим 
. Получим уравнение относительно 
:
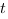Перемножим скобки и перенесем все влево. Получим уравнение третьей степени относительно :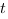
Будем решать это уравнение с помощью понижения степени. Ищем корни уравнения среди делителей числа 70: 
Сумма коэффициентов многочлена не равна нулю, следовательно, число 1 не является корнем уравнения.
Сумма коэффициентов при четных степенях не равна сумме коэффициентов при нечетных степенях, следовательно, число -1 также не является корнем уравнения.
Остальные корни будем проверять с помощью схемы Горнера. 
Итак, 
является корнем многочлена, и многочлен делится на t-5 без остатка:
Чтобы найти остальные корни уравнения 
решим уравнение 
Итак, , 
, .
Вернемся к исходной переменной. ()
1.
2.
3.
Ответ: ; ;
Добавить комментарий