 В этой статье я расскажу, как находить угол между прямой и плоскостью c помощью методом координат.
В этой статье я расскажу, как находить угол между прямой и плоскостью c помощью методом координат.
Для этого нам, как обычно, понадобятся некоторые теоретические сведения.
1. Уравнение плоскости имеет вид 
2. Важно! В этом уравнении плоскости коэффициенты 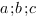 - координаты вектора нормали к плоскости (то есть вектора, перпендикулярного плоскости).
- координаты вектора нормали к плоскости (то есть вектора, перпендикулярного плоскости).
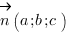
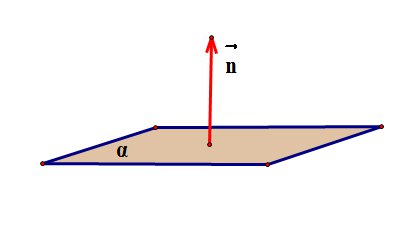
3. Косинус угла между векторами 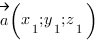 и
и 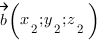 вычисляется по формуле:
вычисляется по формуле:
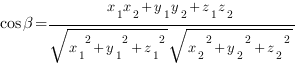
4. Любой ненулевой вектор 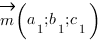 , лежащий на прямой
, лежащий на прямой 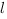 , или параллельный прямой
, или параллельный прямой 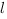 , называется направляющим вектором прямой.
, называется направляющим вектором прямой.
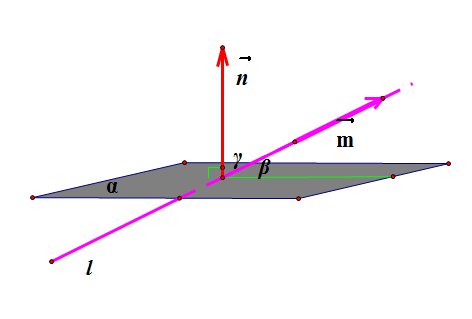
5. Синус угла 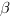 между прямой
между прямой 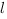 и плоскостью
и плоскостью 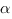 равен косинусу угла
равен косинусу угла 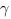 между нормалью (
между нормалью (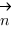 ) к плоскости и направляющим вектором прямой (
) к плоскости и направляющим вектором прямой (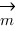 ), поскольку
), поскольку 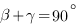
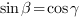
 То есть синус угла
То есть синус угла 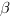 между прямой, направляющий вектор которой имеет координаты
между прямой, направляющий вектор которой имеет координаты 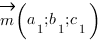 и плоскостью, заданной уравнением
и плоскостью, заданной уравнением  вычисляется по формуле:
вычисляется по формуле:
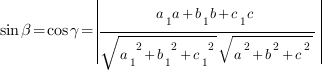
Решим задачу:
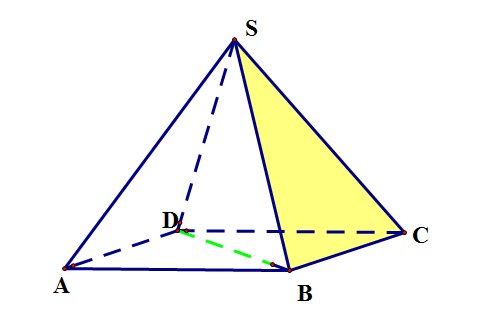
В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, найдите синус угла между прямой BD и плоскостью SBC.
Введем систему координат:
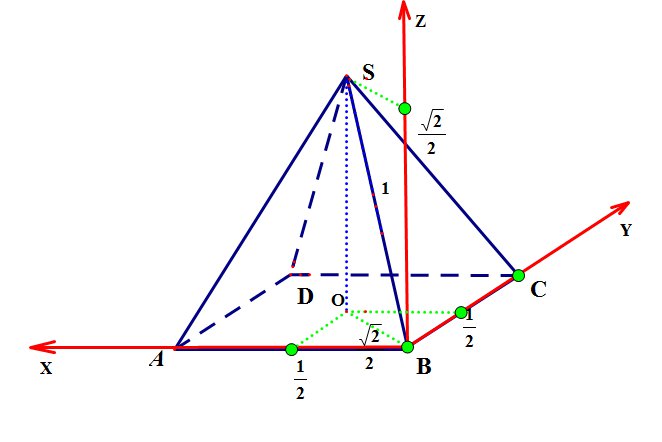
Начало координат поместим в точку В, поэтому все координаты этой точки равны нулю.
Запишем уравнение плоскости SBC. Для этого найдем координаты точек S, B и C и подставим их в уравнение плоскости 
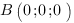
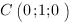 (все ребра пирамиды равны 1)
(все ребра пирамиды равны 1)
Чтобы найти координаты точки S сначала найдем координаты ее проекции на плоскость основания, а затем ее координаты по оси OZ:
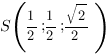
Так как плоскость SBC проходит через начало координат, 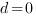 ,
,
Получим систему уравнений:
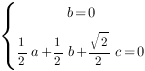
Отсюда 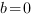 ,
, 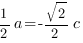 .
.
Уравнение плоскости имеет вид:
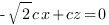 . Разделим обе части равенства на с, получим:
. Разделим обе части равенства на с, получим:
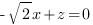 .
.
Таким образом, вектор нормали к плоскости SBC имеет координаты:
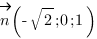
Найдем координаты направляющего вектора прямой BD. Для этого найдем координаты точек B и D, а затем из координат конца вычтем координаты начала.
D(1;1;0)
B(0;0;0), 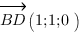
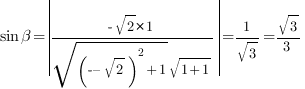
Ответ: 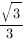

























И все таки никак не выходит составить уравнение плоскости проходящей через начало координат напримерв(0,0,0) а1 (1,0,1)д1 (1,1,1)
Если плоскость проходит через начало координат, d=0. Может так получиться, что количество неизвестных в системе будет больше, чем количество уравнений. В этом случае нужно два неизвестных выразить через третье, например, а и b через с, а потом разделить на с. В вашем случае получается b=0, а=-с. Получается уравнение -сх+0у+сz=0. Делим на с , получаем -х+0у+ z=0. Координаты вектора нормали (-1;0;1)
Подробнее можно уравнение плоскости проходящей через начало координат
А можно эту же задачу решать не через координаты, а через единичные векторы i,j,k, направленные вдоль осей Ox, oy, oz?
Это те же координаты
Тогда как это оформить? Как начать?
Урок неплох, но я, простите, глазом зацепился за одну не совсем правильную формулировку:
«найдем длины проекций точки S на оси координат»
проекцией точки хоть на плоскость, хоть на ось координат является точка. А точка не может иметь длинны.
Cпасибо
Инна Владимировна, простите, кажется, у вас опечатка в последней формуле с синусом — я вместо нее подставила формулу из теории в начале статьи и все получилось) или я что-то неправильно поняла?
ой, извините, знак интеграла неправильно поняла) все сходится
Инна, можете в трёх словах объяснить когда мы должны использовать синус,а когда косинус? я не могу разобраться
Мы можем найти косинус угла между направляющим вектором прямой и вектором нормали. Но нам нужен не этот угол, а угол между направляющим вектором прямой и направляющим вектором проекции этой прямой. Синус угла между направляющим вектором прямой и направляющим вектором проекции этой прямой равен косинусу угла между направляющим вектором прямой и вектором нормали.
Скажите, пожалуйста, почему в первой системе уравнений b =0?
Мы координаты точки С подставили в уравнение плоскости.