 В этой статье я расскажу, как находить угол между прямой и плоскостью c помощью методом координат.
В этой статье я расскажу, как находить угол между прямой и плоскостью c помощью методом координат.
Для этого нам, как обычно, понадобятся некоторые теоретические сведения.
1. Уравнение плоскости имеет вид 
2. Важно! В этом уравнении плоскости коэффициенты 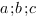 - координаты вектора нормали к плоскости (то есть вектора, перпендикулярного плоскости).
- координаты вектора нормали к плоскости (то есть вектора, перпендикулярного плоскости).
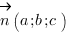
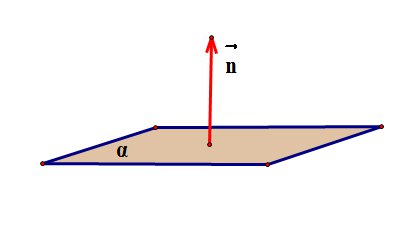
3. Косинус угла между векторами 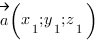 и
и 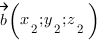 вычисляется по формуле:
вычисляется по формуле:
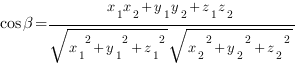
4. Любой ненулевой вектор 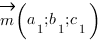 , лежащий на прямой
, лежащий на прямой 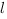 , или параллельный прямой
, или параллельный прямой 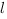 , называется направляющим вектором прямой.
, называется направляющим вектором прямой.
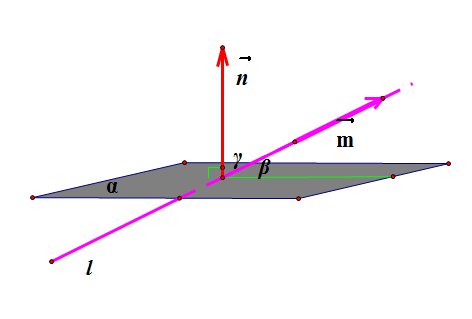
5. Синус угла 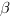 между прямой
между прямой 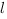 и плоскостью
и плоскостью 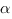 равен косинусу угла
равен косинусу угла 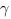 между нормалью (
между нормалью (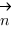 ) к плоскости и направляющим вектором прямой (
) к плоскости и направляющим вектором прямой (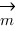 ), поскольку
), поскольку 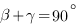
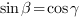
 То есть синус угла
То есть синус угла 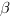 между прямой, направляющий вектор которой имеет координаты
между прямой, направляющий вектор которой имеет координаты 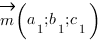 и плоскостью, заданной уравнением
и плоскостью, заданной уравнением  вычисляется по формуле:
вычисляется по формуле:
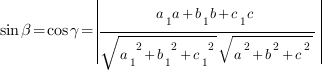
Решим задачу:
В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, найдите синус угла между прямой BD и плоскостью SBC.
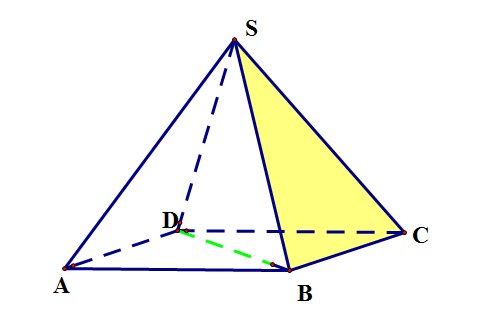
Введем систему координат:
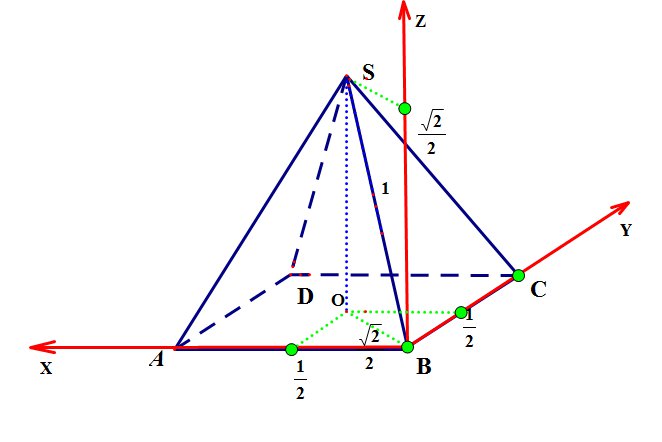
Начало координат поместим в точку В, поэтому все координаты этой точки равны нулю.
Запишем уравнение плоскости SBC. Для этого найдем координаты точек S, B и C и подставим их в уравнение плоскости 
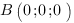
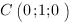 (все ребра пирамиды равны 1)
(все ребра пирамиды равны 1)
Чтобы найти координаты точки S сначала найдем координаты ее проекции на плоскость основания, а затем ее координаты по оси OZ:
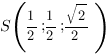
Так как плоскость SBC проходит через начало координат, 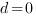 ,
,
Получим систему уравнений:
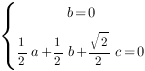
Отсюда 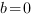 ,
, 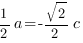 .
.
Уравнение плоскости имеет вид:
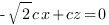 . Разделим обе части равенства на с, получим:
. Разделим обе части равенства на с, получим:
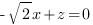 .
.
Таким образом, вектор нормали к плоскости SBC имеет координаты:
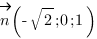
Найдем координаты направляющего вектора прямой BD. Для этого найдем координаты точек B и D, а затем из координат конца вычтем координаты начала.
D(1;1;0)
B(0;0;0), 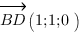
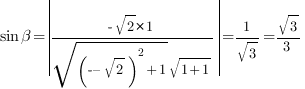
Ответ: 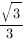

























Инна Владимировна, спасибо Вам огромное! С геометрией у меня всегда были проблемы, а с Вашим сайтом теперь начинаю понемногу её понимать! Объяснения понятные, все разобрано подробно! Чудесный сайт замечательного преподавателя!
например, коорд.дачи 56,4790 с.ш. 36,7765 в.д. высота 175м над ур.моря. спутник Hot Bird висит над меридианом 13,2град. на высоте 42152км от центра Земли. как с дачи его увидеть, на какой высоте и азимуте? очень желательно также учитывать эллипсность земного шара(Земля сплюснута у полюсов на 21км) .
В основании пирамиды SABCD лежит прямоугольник, а её боковое ребро SB перпендикулярно плоскости основания. На рёбрах AB И AD взяты соответственно тачки P,Q — середины этих рёбер. Отношение рёбер пирамиды AB:AD:SB=1:2:1. Найти углы, которые образуют с плоскостью грани SCD и прямой SA
Помогите пожалуйста решить
в прямоугольном параллелепипеде mnpqm1n1p1q1 ребра mn=15 mq=mm1=8 найдите угол между qp1 и плоскостью qpn1
А если бы d не было равно нулю, т.е. если бы плоскость не проходила через начало координат, то как найти d? И в каком случае тогда вместо «a» можно подставлять любое число, как здесь:
Если плоскость не проходит через начало координат, принимаем d=1. вместо «a» можно подставлять любое число, если имеем систему двух уравнений с тремя неизвестными, в этом случае два неизвестных выражаем через третье, а это третье может быть любым числом.
Спасибо большое!